题目内容
设椭圆与双曲线有共同的焦点
 (-4,0)、
(-4,0)、 (4,0),并且椭圆的长轴长是双曲线实轴长的2倍,求椭圆与双曲线的交点的轨迹.
(4,0),并且椭圆的长轴长是双曲线实轴长的2倍,求椭圆与双曲线的交点的轨迹.
答案:略
解析:
解析:
|
解题思路:设 P(x,y)为椭圆、双曲线的交点,双曲线的实半轴长为a,则a<4,从而椭圆的长半轴长为2a,则2a>4.∴a (2,4),由椭圆定义得 (2,4),由椭圆定义得 , ,
由双曲线定义得  . .
∴  , ,
即  , ,
用坐标表示得 
或  , ,
整理得  或 或 .注意到y≠0, .注意到y≠0,
所求轨迹方程为  . . |

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
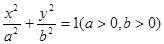 与双曲线
与双曲线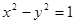 有共同的焦点F1、F2,设它们在第一象限的交点为P,且
有共同的焦点F1、F2,设它们在第一象限的交点为P,且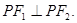
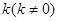 的直线
的直线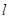 ,与椭圆交于不同的两点A、B,点Q满足
,与椭圆交于不同的两点A、B,点Q满足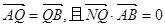 ?若存在,求出
?若存在,求出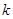 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。