Question

．（本小题满分12分）

    已知椭圆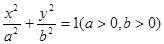与双曲线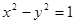有共同的焦点F₁、F₂，设它们在第一象限的交点为P，且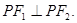

   （1）求椭圆的方程；

   （2）已知N（0，-1），对于（1）中的椭圆，是否存在斜率为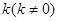的直线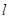，与椭圆交于不同的两点A、B，点Q满足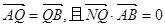？若存在，求出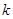的取值范围；若不存在，说明理由。

 

 

Answer 1

【答案】

解：（1）焦点F₁、F₂的坐标分别为、

    由双曲线和椭圆的定义，得

    解得      2分

       

    即   解得     4分

    从而     故椭圆的方程为    6分

   （2）设直线的方程为

    由方程组

    消去得

    直线与椭圆交于不同两点

   

    即①    8分

    则

    由，得Q为线段AB的中点，

    则   

         

    即    化简得     10分

    代入①得解得       11分

    又由

    所以，直线在轴上的截距的取值范围是       12分

 

【解析】略