题目内容
设函数
(1)记集合 ,则
,则 所对应的
所对应的 的零点的取值集合为 .
的零点的取值集合为 .
(2)若 ______.(写出所有正确结论的序号)
______.(写出所有正确结论的序号)
①
②
③若
(1)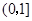 ,(2)①②③;
,(2)①②③;
解析试题分析:(1)因为c>a,由c≥a+b=2a,所以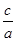 ≥2,则ln
≥2,则ln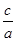 ≥ln2>0.
≥ln2>0.
令f(x)=ax+bx-cx=2ax?cx=cx[2(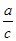 )x?1]=0.得(
)x?1]=0.得(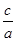 )x=2,
)x=2,
所以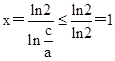 ,所以0<x≤1.
,所以0<x≤1.
故答案为{x|0<x≤1};
(2)因为f(x)=ax+bx?cx=cx[(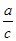 )x+(
)x+(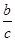 )x?1],
)x?1],
又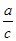 <1,
<1,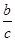 <1,所以对?x∈(-∞,1),(
<1,所以对?x∈(-∞,1),(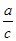 )x+(
)x+(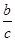 )x?1>(
)x?1>(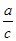 )1+(
)1+(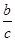 )1?1
)1?1
=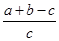 >0.所以命题①正确;
>0.所以命题①正确;
令x=-1,a=2,b=4,c=5.则ax=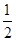 ,bx=
,bx=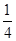 ,cx=
,cx=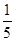 .不能构成一个三角形的三条边长.
.不能构成一个三角形的三条边长.
所以命题②正确;
若三角形为钝角三角形,则a2+b2-c2<0.
f(1)=a+b-c>0,f(2)=a2+b2-c2<0.
所以?x∈(1,2),使f(x)=0.
所以命题③正确.
故答案为①②③.
考点:指数函数的性质,三角形的性质。
点评:难题,判断命题是真命题,应给出严格的证明,说明一个命题是假命题,可以通过举反例,达到解题目的。

练习册系列答案
相关题目
 的定义域为
的定义域为 ,若
,若 且
且 时总有
时总有 ,则称
,则称 是单函数.下列命题:
是单函数.下列命题: 是单函数;
是单函数; 是单函数;
是单函数; ,则
,则 ;
; 在定义域内某个区间
在定义域内某个区间 上具有单调性,则
上具有单调性,则 ,若存在实数
,若存在实数 、
、 、
、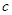 、
、 ,满足
,满足
 ,其中
,其中 ,则
,则 的取值范围是 .
的取值范围是 . ,则满足
,则满足 的
的 的取值范围是______.
的取值范围是______. (
(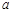 为实数),在区间
为实数),在区间 和
和 上单调递增,则实数
上单调递增,则实数 .
. ,则
,则

 (填“>”或“<”).
(填“>”或“<”).