题目内容
某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示,其中样本数据分组区间为 ,
, ,
, ,
, ,
, .
.

(1)试估计全市学生参加汉字听写考试的平均成绩;
(2)如果从参加本次考试的同学中随机选取1名同学,求这名同学考试成绩在80分以上(含80分)的概率;
(3)如果从参加本次考试的同学中随机选取3名同学,这3名同学中考试成绩在80分以上(含80分)的人数记为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
(注:频率可以视为相应的概率)
(1) ;(2)
;(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)利用各小矩形的底边的中点与高之积的和求其平均数;(2)利用互斥事件的概率公式进行求解;(3)利用二项分布的期望公式进行求解.
试题解析:(1)估计全市学生参加汉字听写考试的平均成绩为:

 . 2分
. 2分
(2)设被抽到的这名同学考试成绩在80分以上为事件A.

答:被抽到的这名同学考试成绩在80分以上的概率为0.4. 6分
(3)由(2)知,从参加考试的同学中随机抽取1名同学的成绩在80分以上的概率为 ,
,
X可能的取值是0,1,2,3.
 ;
;
 ;
;
 ;
;
 .
.
 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
12分
所以  . 13分
. 13分
(或 ,所以
,所以 .).
.).
考点:1.频率分布直方图;2.互斥事件;3.二项分布的概率与期望公式.






 为实数,命题甲:
为实数,命题甲: ,命题乙:
,命题乙: ,则命题甲是命题乙的( )
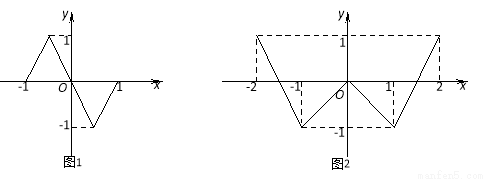
,则命题甲是命题乙的( ) 的定义域为
的定义域为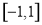 ,图象如图1所示;函数
,图象如图1所示;函数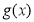 的定义域为
的定义域为 ,图象如图2所示,方程
,图象如图2所示,方程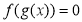 有
有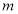 个实数根,方程
个实数根,方程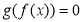 有
有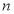 个实数根,则
个实数根,则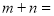 ( )
( ) 
 ,
,  ,则
,则 ( )
( ) B.
B. C.
C. D.
D.

 ,
, ,
, ,那么a等于
,那么a等于 是虚数单位,复数
是虚数单位,复数 的虚部是( )
的虚部是( ) B.
B. C.1 D.-1
C.1 D.-1 所对的边分别是
所对的边分别是 ,且满足:
,且满足: 又
又 .
.