Question

如图所示,点C(a,b)是定点(ab≠0),过点C作两条互相垂直的直线,CA交x轴于A,CB交y轴于B,连结AB,M是AB的中点,求点M的轨迹方程和|MC|的最小值.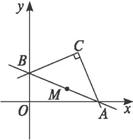

Answer 1

解：设M（x,y）,则点A（2x,0）,B(0,2y),则=(a-2x,b),=(-a,2y-b),由AC⊥CB，∴· =0.

∴-a(a-2x)+b(2y-b)=0,即2ax+2by-(a²+b²)=0,①这就是动点M的轨迹方程.

当|MC|最小时CM垂直于直线①，交点为M，所以|CM|的最小值即为点C到直线①的距离，d=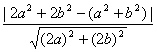=,故|MC|_min=.

注：本题还可设AC的斜率k为参数，消参可求.但要注意讨论斜率k不存在的情形.