Question

14．已知函数f（x）=cosx，x∈（$\frac{π}{2}$，3π），若方程f（x）=m有三个不同的实数根，且三个根α，β，γ（按从小到大排列）满足β²=αγ，则实数m的值可能是-$\frac{1}{2}$．

Answer 1

分析 可设其三个根从小到大依次为α，β，γ，由题意得α+β=2π，β+γ=4π；又α，β，γ成等比数列，可设其公比为q，由①②可解得q的值，从而可求得α、β、γ的值，继而可求得m的值．

解答 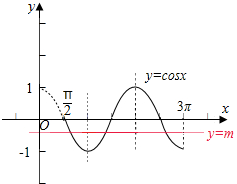解：函数f（x）=cosx，x∈（$\frac{π}{2}$，3π）的图象如图所示：
若方程f（x）=m有三个不同的实数根α，β，γ，
即y=f（x）的图象和直线y=m有三个交点，
且三角交点的横坐标分别为α，β，γ．
再根据三个根α，β，γ（按从小到大排列）满足β²=αγ，
可得α+β=2π，β+γ=4π，且α=$\frac{β}{q}$，γ=βq．
求得q=2，β=$\frac{4π}{3}$，α=$\frac{2π}{3}$，γ=$\frac{8π}{3}$，
则实数m=cos$\frac{2π}{3}$=-$\frac{1}{2}$，
故答案为：-$\frac{1}{2}$．

点评 本题考查数列与三角函数的综合，难点在于α+β=2π，β+γ=4π 的理解，考查了数形结合思想与方程思想，属中档题．