题目内容
已知f(x)=log2x,若2,f(a1),f(a2),f(a3),…,f(an),2n+4,…(n∈N*)成等差数列.
(1)求数列{an}(n∈N*)的通项公式;
(2)设g(k)是不等式 整数解的个数,求g(k);
整数解的个数,求g(k);
(3)在(2)的条件下,试求一个数列{bn},使得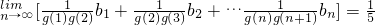 .
.
解:(1)2n+4=2+(n+1)d,
∴d=2 f(an)=2+(n+1-1)•2=2(n+1)
即log2an=2n+2,
∴an=22n+2
(2)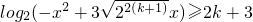 ,
,
∴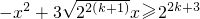 ,
,
得,x2-3•2k+1x+22(k+1)+1≤0,即x2-3•2k+1x+2•(2k+1)2≤0,
∴(x-2k+1)(x-2•2k+1)≤0,
∴2k+1≤x≤2•2k+1
则g(k)=2k+1+1
(3)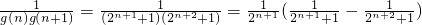 ,
,
取bn=2n+1,
则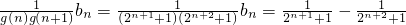
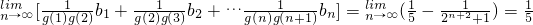 .
.
∴bn=2n+1
分析:(1)先弄清数列的项数,然后根据等差数列的通项公式求出公差d,从而求出f(an)的值,即可求出数列{an}(n∈N*)的通项公式;
(2)将ak代入不等式,然后根据对数的运算性质进行化简变形,然后因式分解得(x-2k+1)(x-2•2k+1)≤0,从而求出x的范围,即可求出g(k);
(3)将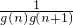 进行裂项得
进行裂项得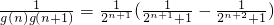 ,可取bn=2n+1,然后验证
,可取bn=2n+1,然后验证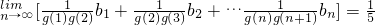 是否成立.
是否成立.
点评:本题主要考查了数列与不等式的综合运用,同时考查了裂项求和法和计算能力,属于中档题.
∴d=2 f(an)=2+(n+1-1)•2=2(n+1)
即log2an=2n+2,
∴an=22n+2
(2)
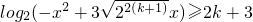 ,
,∴
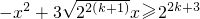 ,
,得,x2-3•2k+1x+22(k+1)+1≤0,即x2-3•2k+1x+2•(2k+1)2≤0,
∴(x-2k+1)(x-2•2k+1)≤0,
∴2k+1≤x≤2•2k+1
则g(k)=2k+1+1
(3)
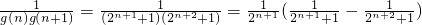 ,
,取bn=2n+1,
则
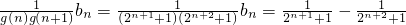
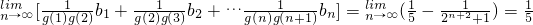 .
.∴bn=2n+1
分析:(1)先弄清数列的项数,然后根据等差数列的通项公式求出公差d,从而求出f(an)的值,即可求出数列{an}(n∈N*)的通项公式;
(2)将ak代入不等式,然后根据对数的运算性质进行化简变形,然后因式分解得(x-2k+1)(x-2•2k+1)≤0,从而求出x的范围,即可求出g(k);
(3)将
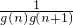 进行裂项得
进行裂项得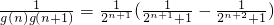 ,可取bn=2n+1,然后验证
,可取bn=2n+1,然后验证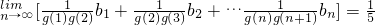 是否成立.
是否成立.点评:本题主要考查了数列与不等式的综合运用,同时考查了裂项求和法和计算能力,属于中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知f(x)是定义在R上的奇函数,当x>0时,f(x)=log
x,那么f(-
)的值是( )
| 1 |
| 4 |
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |