题目内容
已知过点O的直线与函数y=2x的图象交于A、B两点,点A在线段OB上,过A作y轴的平行线交函数y=4x的图象于C点,当BC∥x轴,点A的横坐标是
1
1
.分析:设点A、B的横坐标分别为x1、x2则点A、B纵坐标分别为2x1 、2x2 ,解出C的坐标,根据条件求出x1与x2的等量关系,然后根据OA、OB的斜率相等建立等式关系,求出所求即可.
解答:解:设点A、B的横坐标分别为x1、x2则点A、B纵坐标分别为2x1、2x2.
因为A、B在过点O的直线上,所以
=
.
∵过A作y轴的平行线交函数y=4x的图象于C点,∴点C(x1,4x1).
而BC∥x轴,∴4x1=2x2 即 2x1=x2,将2x1=x2代入
=
,可得 (2x1)2=2×2x1,
解得 x1=1. 于是点A的横坐标为 1,
故答案为 1.
因为A、B在过点O的直线上,所以
| 2x1 |
| x1 |
| 2x2 |
| x2 |
∵过A作y轴的平行线交函数y=4x的图象于C点,∴点C(x1,4x1).
而BC∥x轴,∴4x1=2x2 即 2x1=x2,将2x1=x2代入
| 2x1 |
| x1 |
| 2x2 |
| x2 |
解得 x1=1. 于是点A的横坐标为 1,
故答案为 1.
点评:本小题主要考查指数函数图象、指数方程等基础知识,考查运算能力和分析问题的能力,属于中档题.

练习册系列答案
相关题目
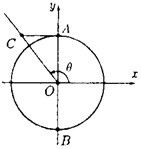 如图,已知单位圆O与y轴相交于A、B两点.角θ的顶点为原点,始边在x轴的正半轴上,终边在射线OC上.过点A作直线AC垂直于y轴且与角θ的终边交于点C,则有向线段AC的函数值是( )
如图,已知单位圆O与y轴相交于A、B两点.角θ的顶点为原点,始边在x轴的正半轴上,终边在射线OC上.过点A作直线AC垂直于y轴且与角θ的终边交于点C,则有向线段AC的函数值是( )| A、sinθ | B、cosθ | C、tanθ | D、cotθ |
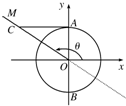 如图所示,已知单位圆O与y轴交于A、B两点,角θ的顶点为原点,始边在x轴的非负半轴上,终边在射线OM上,过点A作直线AC垂直于y轴与角θ的终边OM交于点C,则有向线段AC表示的函数值是什么?
如图所示,已知单位圆O与y轴交于A、B两点,角θ的顶点为原点,始边在x轴的非负半轴上,终边在射线OM上,过点A作直线AC垂直于y轴与角θ的终边OM交于点C,则有向线段AC表示的函数值是什么?

