题目内容
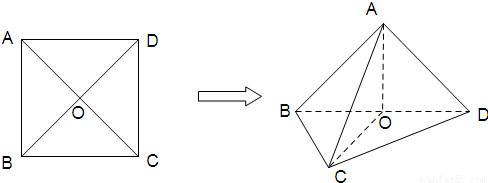
三棱锥A-BCD，AB=a，CD=b，∠ABD=∠BDC，M，N分别为AD，BC的中点，P为BD上一点，则MP+NP 的最小值是________．
分析：如图，可以将三棱锥A-BCD沿着线段BD展开成平面图形，由于，∠ABD=∠BDC，可得出展开图中AB∥CD，连接MN与BD交点为P，此时必有P是中点，由此可求出MP+NP 的最小值
解答：
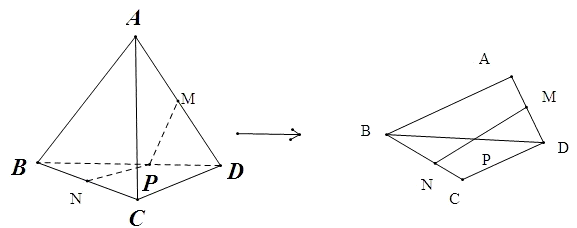解：由题意，将三棱锥A-BCD沿着线段BD展开成平面图形，由于，∠ABD=∠BDC，可得出展开图中AB∥CD，连接MN与BD交点为P，此时必有P是中点，由两点间线段最短知，当P点是BD中点时，MP+NP 的值最小当P是中点时，MP是AB的一半，NP是CD的一半，又，AB=a，CD=b，
故可得出MP+NP 的最小值是
故答案为
点评：本题考查棱锥的结构特征，解答本题关键是根据将立体图形转化为平面图形，再由平面上两点间线段最短确定出点P的位置，从而求出MP+NP 的最小值，在研究几何体表面上的两点间距离最短的问题时，展开求最小距离是一个经常采用的技巧．此类问题常借助图形进行研究，作出符合题意的图象是正确解答的保证．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
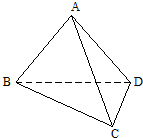已知三棱锥A-BCD，平面ABD⊥平面BCD，AB=AD=1，AB⊥AD，DB=DC，DB⊥DC 
如图，将正方形ABCD沿对角线BD折成直二面角，连接A′C得到三棱锥A′-BCD，A′F 垂直BD于F，E为BC的中点．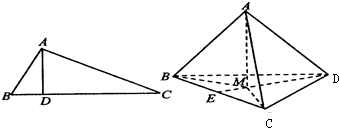
如图，在△ABC中，AB⊥AC，若AD⊥BC，则AB2=BD•BC；类似地有命题：在三棱锥A-BCD中，AD⊥面ABC，若A点在BCD内的射影为M，则有