题目内容
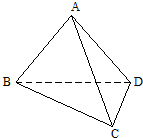 已知三棱锥A-BCD,平面ABD⊥平面BCD,AB=AD=1,AB⊥AD,DB=DC,DB⊥DC
已知三棱锥A-BCD,平面ABD⊥平面BCD,AB=AD=1,AB⊥AD,DB=DC,DB⊥DC (1)求证:AB⊥平面ADC;
(2)求三棱锥A-BCD的体积;
(3)求二面角A-BC-D的正切值.
分析:(1)由平面ABD⊥平面BCD且DB⊥DC,利用面面垂直的性质定理证出CD⊥平面ABD,从而得到CD⊥AB,结合AB⊥AD利用线面垂直判定定理,即可证出AB⊥平面ADC.
(2)取BD的中点O,连结AO,等腰Rt△ABD中证出A0⊥BD,进而根据平面ABD⊥平面BCD证出A0⊥平面BCD,可得AO是三棱锥A-BCD的高,再根据题中数据利用锥体体积公式加以计算,可得三棱锥A-BCD的体积;
(3)过O作OE⊥BC于点E,连结AE,根据三垂线定理证出AE⊥BC,从而可得∠AEO为二面角A-BC-D的平面角.Rt△AEO中算出OE=
,根据AO=
利用正切的定义算出tan∠AEO=
,即得二面角A-BC-D的正切值.
(2)取BD的中点O,连结AO,等腰Rt△ABD中证出A0⊥BD,进而根据平面ABD⊥平面BCD证出A0⊥平面BCD,可得AO是三棱锥A-BCD的高,再根据题中数据利用锥体体积公式加以计算,可得三棱锥A-BCD的体积;
(3)过O作OE⊥BC于点E,连结AE,根据三垂线定理证出AE⊥BC,从而可得∠AEO为二面角A-BC-D的平面角.Rt△AEO中算出OE=
| 1 |
| 2 |
| ||
| 2 |
| 2 |
解答:解:(1)∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,DB⊥DC.
∴CD⊥平面ABD,
∵AB?平面ABD,∴CD⊥AB,
又∵AB⊥AD,且AD∩AB=B,∴AB⊥平面ADC.
(2)取BD的中点O,连结AO,
∵AB=AD=1,AB⊥AD,∴△ABD为等腰直角三角形,
∴A0⊥BD,且AO=
,BD=
.
∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,A0⊥BD,
∴A0⊥平面BCD,即AO是三棱锥A-BCD的高,
∵DB=DC,DB⊥DC.∴CD=BD=
,
即△BCD的面积S=
×
×
=1,
∴三棱锥A-BCD的体积V=
×S×AO=
×1×
=
.
(3)过O作OE⊥BC于点E,连结AE,
∵AO⊥平面BCD,可得OE是AE在平面BCD内的射影,
∴AE⊥BC,可得∠AEO为二面角A-BC-D的平面角.
Rt△BOE中,BO=
,∠OBE=45°,可得OE=BOsin45°=
,
∴Rt△AEO中,tan∠AEO=
=
,即得二面角A-BC-D的正切值等于
.
∴CD⊥平面ABD,

∵AB?平面ABD,∴CD⊥AB,
又∵AB⊥AD,且AD∩AB=B,∴AB⊥平面ADC.
(2)取BD的中点O,连结AO,
∵AB=AD=1,AB⊥AD,∴△ABD为等腰直角三角形,
∴A0⊥BD,且AO=
| ||
| 2 |
| 2 |
∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,A0⊥BD,
∴A0⊥平面BCD,即AO是三棱锥A-BCD的高,
∵DB=DC,DB⊥DC.∴CD=BD=
| 2 |
即△BCD的面积S=
| 1 |
| 2 |
| 2 |
| 2 |
∴三棱锥A-BCD的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
(3)过O作OE⊥BC于点E,连结AE,
∵AO⊥平面BCD,可得OE是AE在平面BCD内的射影,
∴AE⊥BC,可得∠AEO为二面角A-BC-D的平面角.
Rt△BOE中,BO=
| ||
| 2 |
| 1 |
| 2 |
∴Rt△AEO中,tan∠AEO=
| AO |
| OE |
| 2 |
| 2 |
点评:本题在给定三棱锥中求证线面垂直,并求二面角的正切值与锥体的体积.着重考查了面面垂直的性质、线面垂直的判定与性质、锥体的体积公式和二面角的平面角的定义及求法等知识,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
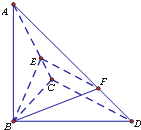 已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且
已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且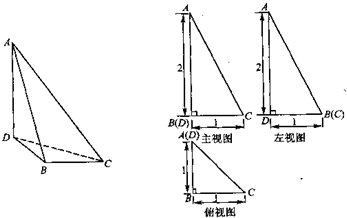 (2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.
(2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.