题目内容
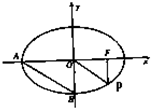
点P是椭圆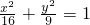 上一点,F1、F2是其焦点,若∠F1PF2=90°,△F1PF2面积为________.
上一点,F1、F2是其焦点,若∠F1PF2=90°,△F1PF2面积为________.
9
分析:根据椭圆方程算出c= =
= ,从而Rt△F1PF2中得到|PF1|2+|PF2|2=28,结合椭圆的定义联解,得到|PF1|•|PF2|=18,最后用直角三角形面积公式,即可算出△F1PF2的面积.
,从而Rt△F1PF2中得到|PF1|2+|PF2|2=28,结合椭圆的定义联解,得到|PF1|•|PF2|=18,最后用直角三角形面积公式,即可算出△F1PF2的面积.
解答:∵椭圆方程为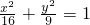 ,
,
∴a2=16,b2=9.可得c= =
=
因此Rt△F1PF2中,|F1F2|=2 ,由勾股定理得
,由勾股定理得
|PF1|2+|PF2|2=( )2=28…①
)2=28…①
根据椭圆的定义,得|PF1|+|PF2|=2a=8…②
①②联解,可得|PF1|•|PF2|=18
∴△F1PF2面积S= |PF1|•|PF2|=9
|PF1|•|PF2|=9
故答案为:9
点评:本题给出椭圆方程,求当焦点三角形是直角三角形时求焦点三角形的面积,着重考查了勾股定理、椭圆的标准方程与简单性质等知识,属于基础题.
分析:根据椭圆方程算出c=
 =
= ,从而Rt△F1PF2中得到|PF1|2+|PF2|2=28,结合椭圆的定义联解,得到|PF1|•|PF2|=18,最后用直角三角形面积公式,即可算出△F1PF2的面积.
,从而Rt△F1PF2中得到|PF1|2+|PF2|2=28,结合椭圆的定义联解,得到|PF1|•|PF2|=18,最后用直角三角形面积公式,即可算出△F1PF2的面积.解答:∵椭圆方程为
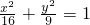 ,
,∴a2=16,b2=9.可得c=
 =
=
因此Rt△F1PF2中,|F1F2|=2
 ,由勾股定理得
,由勾股定理得|PF1|2+|PF2|2=(
 )2=28…①
)2=28…①根据椭圆的定义,得|PF1|+|PF2|=2a=8…②
①②联解,可得|PF1|•|PF2|=18
∴△F1PF2面积S=
 |PF1|•|PF2|=9
|PF1|•|PF2|=9故答案为:9
点评:本题给出椭圆方程,求当焦点三角形是直角三角形时求焦点三角形的面积,着重考查了勾股定理、椭圆的标准方程与简单性质等知识,属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 已知椭圆
已知椭圆