题目内容
(本小题满分13分)已知函数f (x)=ln x-a2x2+ax (a∈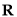 ).
).
(1)当a=1时,求函数f (x)的单调区间;
(2)若函数f (x)在区间 (1,+∞)上是减函数,求实数a的取值范围.
(1)函数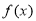 的单调递增区间是
的单调递增区间是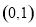 ,单调递减区间是
,单调递减区间是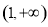 ;
;
(2)实数a的取值范围是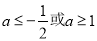 .
.
【解析】
试题分析:(1)当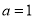 时,
时,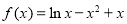 ,定义域是
,定义域是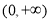 .首先求得:
.首先求得: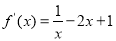 ,再利用导数的符号判断函数
,再利用导数的符号判断函数 的单调性并求单调区间;
的单调性并求单调区间;
(2)首先求出函数 的导数
的导数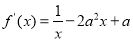 ,因为函数f (x)在区间 (1,+∞)上是减函数,所以所以
,因为函数f (x)在区间 (1,+∞)上是减函数,所以所以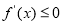 在
在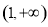 上恒成立;转化为二次函数、二次方程与二次不等式问题.
上恒成立;转化为二次函数、二次方程与二次不等式问题.
试题解析:【解析】
(Ⅰ)当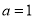 时,
时,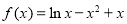 ,定义域是
,定义域是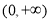 .
.
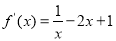 ,
,
由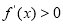 ,解得
,解得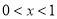 ;由
;由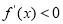 ,解得
,解得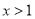 ;
;
所以函数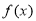 的单调递增区间是
的单调递增区间是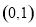 ,单调递减区间是
,单调递减区间是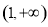 . 5分
. 5分
(2)(法一)
因为函数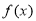 在区间
在区间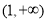 上是减函数,所以
上是减函数,所以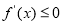 在
在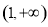 上恒成立,
上恒成立,
则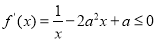 ,即
,即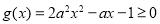 在
在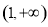 上恒成立. 7分
上恒成立. 7分
当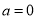 时,
时,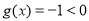 ,所以
,所以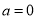 不成立. 9分
不成立. 9分
当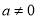 时,
时,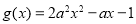 ,
,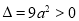 ,对称轴
,对称轴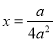 .
.
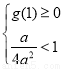 ,即
,即 ,解得
,解得
所以实数a的取值范围是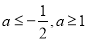 . 13分
. 13分
(法二)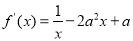
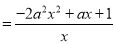 ,定义域是
,定义域是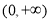 .
.
①当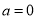 时,
时, 在区间
在区间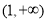 上是增函数,所以
上是增函数,所以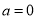 不成立. 8分
不成立. 8分
②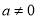 时,
时,
令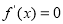 ,即
,即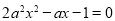 ,则
,则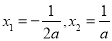 , 9分
, 9分
(1)当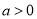 时,由
时,由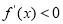 ,解得
,解得 ,
,
所以函数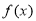 的单调递减区间是
的单调递减区间是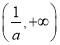 .
.
因为函数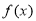 在区间
在区间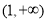 上是减函数,+所以
上是减函数,+所以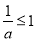 ,解得
,解得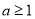 . 11分
. 11分
(2)当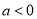 时,由
时,由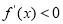 ,解得
,解得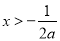 ,
,
所以函数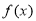 的单调递减区间是
的单调递减区间是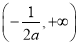 .
.
因为函数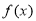 在区间
在区间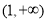 上是减函数,所以
上是减函数,所以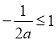 ,解得
,解得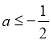 .
.
综上实数a的取值范围是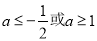 . 13分
. 13分
考点:1、导数在研究函数性质中的应用;2、二次函数、二次方程与一元二次不等式综合问题;3、等价转化的思想与数形结合的思想.

练习册系列答案
相关题目
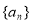 中,
中,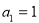 ,且
,且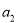 是
是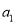 和
和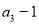 的等差中项.
的等差中项.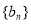 满足
满足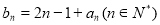 ,求
,求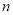 项和
项和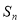 .
. 中,
中, 和
和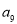 是关于方程
是关于方程 的两根,则该数列的前11项和
的两根,则该数列的前11项和 ( )
( ) ,那么输出的结果是 ,如果输入
,那么输出的结果是 ,如果输入 ,那么输出的结果是 .
,那么输出的结果是 .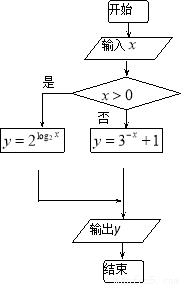
 中,
中, ,则
,则 等于
等于 B.
B. C.
C. D.
D.
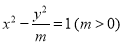 的离心率是2,则
的离心率是2,则 以该双曲线的右焦点为圆心且与其渐近线相切的圆的方程是 .
以该双曲线的右焦点为圆心且与其渐近线相切的圆的方程是 .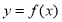 的定义域为[1,5],则函数
的定义域为[1,5],则函数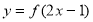 的定义域是( )
的定义域是( ) ,在
,在 轴、
轴、 轴上的截距分别为
轴上的截距分别为 ,且满足
,且满足 的直线方程为 .
的直线方程为 .