题目内容
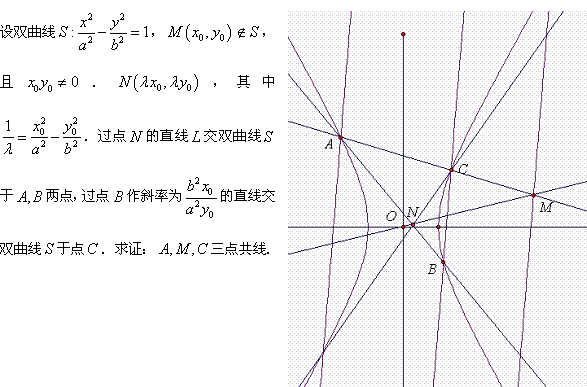
证:设![]() ,
,![]() ,
,![]() .过点
.过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() ,则直线
,则直线![]() 的方程为
的方程为
![]() ①
①
设直线![]() 交
交![]() 与点
与点![]() 、交
、交![]() 于点
于点![]() ,
,![]() 为
为![]() 中点.
中点.
由![]() 得:
得:
![]() ,
,![]() .
.
两式相减后化简后可得:
![]() .
.
∴ ![]() 在直线
在直线![]() 上。从而
上。从而![]() 为
为![]() 中点.
中点.
设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ②
②
故![]() 是方程
是方程![]() 的两根.整理得:
的两根.整理得:
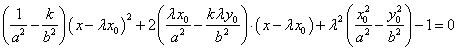
将![]() 代入上式,得:
代入上式,得:
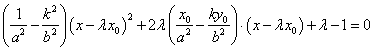
将其视为关于![]() 的一元二次方程.由韦达定理,有
的一元二次方程.由韦达定理,有
![]() ③
③
联立①②,消去![]() 得到
得到![]() .
.
比较③式得:![]() .
.
从而 ![]() .
.
下面利用平几知识证明![]() 三点共线.
三点共线.
首先假设![]() 三点共线,来证明:
三点共线,来证明:![]() .
.
过![]() 做直线
做直线![]() ∥
∥![]() ,交
,交![]() 与
与![]() .设
.设![]() 为
为![]() 中点.
中点.
由于![]() ∥
∥![]() ∥
∥![]() ,∴
,∴ ![]() 的中点
的中点![]() 共线(过点
共线(过点![]() ).
).
∴ ![]() .整理即得:
.整理即得:![]() .
.
反之,用同一法可证明当![]() 时
时![]() 三点共线.
三点共线.

练习册系列答案
相关题目
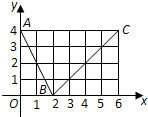 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=