题目内容
已知函数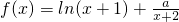
(1)当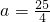 时,求f(x)的单调递减区间;
时,求f(x)的单调递减区间;
(2)若当x>0时,f(x)>1恒成立,求a的取值范围;
(3)求证: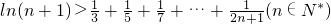 .
.
(1)解:当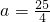 时,
时, (x>-1)
(x>-1)
令f′(x)<0,可得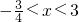 ,∴f(x)的单调递减区间为
,∴f(x)的单调递减区间为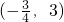 …(4分)
…(4分)
(2)解:由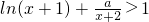 得a>(x+2)-(x+2)ln(x+1)
得a>(x+2)-(x+2)ln(x+1)
记g(x)=(x+2)[1-ln(x+1)],则
当x>0时 g′(x)<0,∴g(x)在(0,+∞)递减
又g(0)=2•[1-ln1]=2,∴g(x)<2(x>0),∴a≥2…(8分)
(3)证明:由(Ⅱ)知 (x>0)
(x>0)
∴
取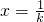 得
得 ,即
,即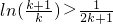
∴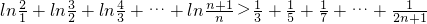 …(12分)
…(12分)
分析:(1)求导数,利用导数小于0,即可求f(x)的单调递减区间;
(2)由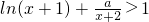 得a>(x+2)-(x+2)ln(x+1),记g(x)=(x+2)[1-ln(x+1)],确定函数的最值,即可求a的取值范围;
得a>(x+2)-(x+2)ln(x+1),记g(x)=(x+2)[1-ln(x+1)],确定函数的最值,即可求a的取值范围;
(3)先证明 ,取
,取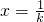 ,即可证得结论.
,即可证得结论.
点评:本题考查导数知识的运用,考查函数的单调性,考查不等式的证明,属于中档题.
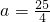 时,
时, (x>-1)
(x>-1)令f′(x)<0,可得
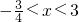 ,∴f(x)的单调递减区间为
,∴f(x)的单调递减区间为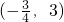 …(4分)
…(4分)(2)解:由
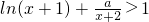 得a>(x+2)-(x+2)ln(x+1)
得a>(x+2)-(x+2)ln(x+1)记g(x)=(x+2)[1-ln(x+1)],则

当x>0时 g′(x)<0,∴g(x)在(0,+∞)递减
又g(0)=2•[1-ln1]=2,∴g(x)<2(x>0),∴a≥2…(8分)
(3)证明:由(Ⅱ)知
 (x>0)
(x>0)∴

取
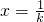 得
得 ,即
,即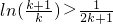
∴
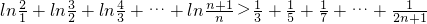 …(12分)
…(12分)分析:(1)求导数,利用导数小于0,即可求f(x)的单调递减区间;
(2)由
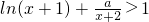 得a>(x+2)-(x+2)ln(x+1),记g(x)=(x+2)[1-ln(x+1)],确定函数的最值,即可求a的取值范围;
得a>(x+2)-(x+2)ln(x+1),记g(x)=(x+2)[1-ln(x+1)],确定函数的最值,即可求a的取值范围;(3)先证明
 ,取
,取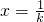 ,即可证得结论.
,即可证得结论.点评:本题考查导数知识的运用,考查函数的单调性,考查不等式的证明,属于中档题.

练习册系列答案
相关题目
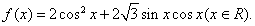
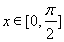
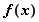

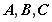
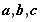
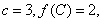
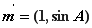
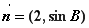
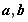

 时,求函数的最大值和最小值;
时,求函数的最大值和最小值; 的取值范围,使
的取值范围,使 在区间
在区间 上是单调减函数
上是单调减函数 .(
.( ).
). 时,求函数
时,求函数 的极值;
的极值; (2)若对
(2)若对 ,有成立,求实数
,有成立,求实数 的取值范围.
的取值范围.
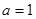 时,求
时,求 的极小值;
的极小值; ,求
,求 的最大值
的最大值 .
.