题目内容
已知 均为正数,证明:
均为正数,证明: .
.
证明见解析.
解析试题分析:不等式是对称式,特别是本题中不等式成立的条件是
 ,因此我们可以用基本不等式,注意对称式的应用,如
,因此我们可以用基本不等式,注意对称式的应用,如 ,对应的有
,对应的有 ,
, ,这样可得
,这样可得 ①,同样方法可得
①,同样方法可得 ,因此有
,因此有 ②,①②相加,再应用基本不等式就可证明本题不等式了.
②,①②相加,再应用基本不等式就可证明本题不等式了.
因为a,b,c均为正数,
由均值不等式得a2+b2≥2ab, b2+c2≥2bc, c2+a2≥2ac.
所以a2+b2+c2≥ab+bc+ac.同理 ,
,
故a2+b2+c2+ ≥ab+bc+ac+
≥ab+bc+ac+ ≥6
≥6 .
.
所以原不等式成立. 10分
考点:不等式的证明.

练习册系列答案
相关题目
 的不等式
的不等式 ,其中常数
,其中常数 是实数.
是实数. 的最小值为
的最小值为 .
. 为正实数,且
为正实数,且 ,求证:
,求证: .
. .
.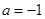 ,
, ,
, 时,求
时,求 的解集;
的解集;  ,且当
,且当 时,
时, 的最小值.
的最小值. .
. ;
; 时, 不等式
时, 不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. =
=
 2;
2; ,求
,求 的取值范围.
的取值范围.