题目内容
已知函数
.
（1）解不等式：
；
（2）当
时， 不等式
恒成立，求实数
的取值范围.
（1）
； （2）
解析试题分析：（1）由函数，及解不等式，通过将x的区间分为3类可解得结论.
（2）由当时， 不等式恒成立，令函数
.所以原题等价于
，由
.通过绝对值不等式的公式即可得到函数
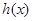的最大值，再通过解绝对值不等式可得结论.
（1）原不等式等价于：
当
时，
，即
.
当
时，
，即
当
时，
，即
.
综上所述，原不等式的解集为. 4分
（2）当时，
=
所以
7分
考点：1.绝对值不等式.2.恒成立问题.3.分类的数学思想.
练习册系列答案
高中必刷题系列答案
相关题目
.
时，求
的解集；
时，
的集合.
均为正数，证明：
．
2｜x－3｜＋｜x－4｜．
的解集；
的解集不是空集，求实数a的取值范围．
的
的取值范围是________.
；
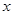的不等式: 
.
+
+
≥
+
+
.
，则x＋y＋z＝________.