题目内容
已知 是直线
是直线 上的动点,
上的动点,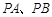 是圆
是圆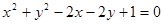 的切线,
的切线, 是切点,
是切点,  是圆心,那么四边形
是圆心,那么四边形 面积的最小值是( )
面积的最小值是( )
 是直线
是直线 上的动点,
上的动点,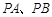 是圆
是圆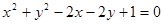 的切线,
的切线, 是切点,
是切点,  是圆心,那么四边形
是圆心,那么四边形 面积的最小值是( )
面积的最小值是( )A.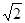 | B. | C. | D.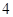 |
C
解:∵圆的方程为:x2+y2-2x-2y+1=0
∴圆心C(1,1)、半径r为:1
根据题意,若四边形面积最小
当圆心与点P的距离最小时,距离为圆心到直线的距离时,
切线长PA,PB最小
圆心到直线的距离为d=3
∴|PA|="|PB|=" ∴sPACB=2×
∴sPACB=2× |PA|r=
|PA|r= 
故答案为选C。
∴圆心C(1,1)、半径r为:1
根据题意,若四边形面积最小
当圆心与点P的距离最小时,距离为圆心到直线的距离时,
切线长PA,PB最小
圆心到直线的距离为d=3
∴|PA|="|PB|="
 ∴sPACB=2×
∴sPACB=2× |PA|r=
|PA|r= 
故答案为选C。

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 的参数方程是
的参数方程是 ,圆C的极坐标方程为
,圆C的极坐标方程为 .
. 与圆
与圆 ,则圆
,则圆 与圆
与圆 的位置关系为( )
的位置关系为( )
 轴相切,圆心在直线
轴相切,圆心在直线 上,则此圆方程为 .
上,则此圆方程为 .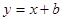 与曲线
与曲线 恰有一个公共点,
恰有一个公共点, 的取值范围是 。
的取值范围是 。 上的点到直线x-y=2的距离的最大值是( )
上的点到直线x-y=2的距离的最大值是( ) 



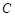 的圆心在双曲线
的圆心在双曲线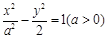 的右焦点且与此双曲线的渐近线相切,若圆
的右焦点且与此双曲线的渐近线相切,若圆 截得的弦长等于
截得的弦长等于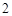 ,则
,则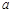 的值为( )
的值为( )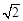
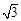
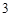
 =2
=2 ,则
,则 ·
· =________.
=________.