题目内容
6.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,且经过点(1,$\frac{3}{2}$).(Ⅰ)求椭圆C的方程;
(Ⅱ)设椭圆的短轴两端点分别为A,B,过椭圆C外一点T(0,m)是否存在一条直线l交椭圆C于P,Q两点,使得$\overrightarrow{TP}$•$\overrightarrow{TQ}$=$\frac{7}{6}$$\overrightarrow{TA}$•$\overrightarrow{TB}$?若存在,请求出此直线;若不存在,请说明理由.
分析 (Ⅰ)由椭圆离心率为$\frac{1}{2}$,且经过点(1,$\frac{3}{2}$),列出方程组,能求出a2=4,b2=3,由此能求出椭圆C的方程.
(Ⅱ)设直线l的方程为y=kx+m,联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3+4k2)x2+8kmx+4m2-12=0,利用根的判别式、韦达定理、向量数量积,结合已知条件能求出过椭圆C外一点T(0,m)存在一条直线l交椭圆C于P,Q两点,使得$\overrightarrow{TP}$•$\overrightarrow{TQ}$=$\frac{7}{6}$$\overrightarrow{TA}$•$\overrightarrow{TB}$,并能求出此直线方程.
解答 解:(Ⅰ)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,
且经过点(1,$\frac{3}{2}$),
∴$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{1}{2}}\\{\frac{1}{{a}^{2}}+\frac{9}{4{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a2=4,b2=3,
∴椭圆C的方程是$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(Ⅱ)设过椭圆C外一点T(0,m)存在一条直线l交椭圆C于P,Q两点,
∴设直线l的方程为y=kx+m,
联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3+4k2)x2+8kmx+4m2-12=0,
△=64k2m2-4(3+4k2)(4m2-12)>0,
设P(x1,y1),Q(x2,y2),则${x}_{1}+{x}_{2}=-\frac{8km}{3+4{k}^{2}}$,x1x2=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$,
∵椭圆的短轴两端点分别为A(0,$\sqrt{3}$),B(0,-$\sqrt{3}$),椭圆C外一点T(0,m),
$\overrightarrow{TP}$•$\overrightarrow{TQ}$=$\frac{7}{6}$$\overrightarrow{TA}$•$\overrightarrow{TB}$,
∴(x1,y1-m)•(x2,y2-m)=$\frac{7}{6}$(0,$\sqrt{3}$-m)•(0,-$\sqrt{3}$-m),
即(k2+1)x1x2=$\frac{7}{6}({m}^{2}-3)$,
∴$({k}^{2}+1)×\frac{4{m}^{2}-12}{3+4{k}^{2}}$=$\frac{7}{6}({m}^{2}-3)$,
解得k=$±\frac{\sqrt{3}}{2}$,
∴过椭圆C外一点T(0,m)存在一条直线l交椭圆C于P,Q两点,使得$\overrightarrow{TP}$•$\overrightarrow{TQ}$=$\frac{7}{6}$$\overrightarrow{TA}$•$\overrightarrow{TB}$,
此直线方程为y=$±\frac{\sqrt{3}}{2}x+m$.
点评 本题考查椭圆方程的求法,考查满足条件的直线方程是否存在的探究与求法,考查推理谁论证能力、数据处理能力、运算求解能力,考查转化思想、化归思想,是中档题.

 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案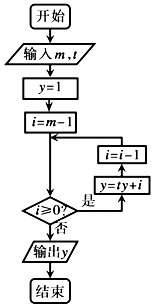
| A. | 61 | B. | 62 | C. | 183 | D. | 184 |
| A. | y=2x+3 | B. | y=2x-3 | C. | y=-2x+3 | D. | y=-2x-3 |
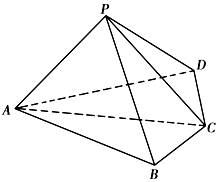 如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.
如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.