题目内容
定义在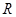 上的函数
上的函数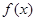 满足
满足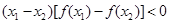 ,若
,若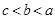 ,
,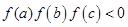 ,实数
,实数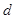 是函数
是函数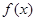 的一个零点.给出下列四个判断:
的一个零点.给出下列四个判断:
①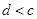 ; ②
; ②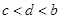 ; ③
; ③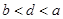 ; ④
; ④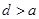 .
.
其中可能成立的个数为 ( )
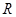 上的函数
上的函数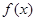 满足
满足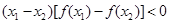 ,若
,若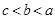 ,
,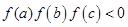 ,实数
,实数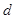 是函数
是函数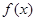 的一个零点.给出下列四个判断:
的一个零点.给出下列四个判断:①
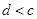 ; ②
; ②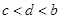 ; ③
; ③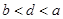 ; ④
; ④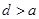 .
.其中可能成立的个数为 ( )
| A.1 | B.2 | C.3 | D.4 |
B
本题考查函数单调性的判定和应用。
从
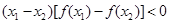 知
知 单调递减。
单调递减。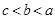 ,
,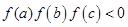 ,讨论函数值的符号,可以得到两种满足的情况,分别是
,讨论函数值的符号,可以得到两种满足的情况,分别是 和
和 。
。所以
 的值可以判断,有两种情况,分别是①③
的值可以判断,有两种情况,分别是①③故选B

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
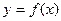 的图象关于
的图象关于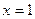 对称,当
对称,当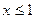 时
时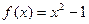 ;
;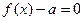 (
(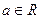 )的根的情况.
)的根的情况. 在
在 处连续,则
处连续,则


 ,函数
,函数 ,
, (Ⅰ)当
(Ⅰ)当 =2时,写出函数
=2时,写出函数 的单调递增区间;
的单调递增区间; (Ⅱ)当
(Ⅱ)当 上的最小值;
上的最小值; ,函数
,函数 在
在 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出 的取值范围(用
的取值范围(用 ,则
,则 (10)值为( )
(10)值为( )
 ,若
,若 且
且 .
. .
. ,若
,若 ,则
,则 的值是( )
的值是( ) B
B  C
C  D
D 
 那么不等式
那么不等式 的解集为 。
的解集为 。 上连续不断,定义:
上连续不断,定义: ,
, ,其中,
,其中, 表示函数
表示函数 在
在 上的最小值,
上的最小值, 表示函数
表示函数 对任意的
对任意的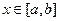 成立,则称函数
成立,则称函数 上的“
上的“ 阶收缩函数” .
阶收缩函数” . 为[-1,4]上的“
为[-1,4]上的“