题目内容
设空间四点O,A,B,P满足
=m
+n
,其中m+n=1,则( )
| OP |
| OA |
| OB |
分析:由题意可得m=1-n,代入向量式化简可得
=n
,可得向量共线,进而可得三点共线,可得结论.
| AP |
| AB |
解答:解:已知m+n=1,则m=1-n,
故有
=(1-n)
+n
=
-n
+n
可得
-
=n(
-
),即
=n
.
因为
≠0,所以
和
共线,即点A,P,B共线,
故选A
故有
| OP |
| OA |
| OB |
| OA |
| OA |
| OB |
可得
| OP |
| OA |
| OB |
| OA |
| AP |
| AB |
因为
| AB |
| AP |
| AB |
故选A
点评:本题考查平面向量的共线问题,熟练表示出向量共线的条件是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设空间四点O,A,B,P,满足
=
+t
,其中0<t<1,则有( )
| OP |
| OA |
| AB |
| A、点P在线段AB上 |
| B、点P在线段AB的延长线上 |
| C、点P在线段BA的延长线上 |
| D、点P不一定在直线AB上 |
 =m
=m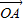 +n
+n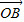 ,其中m+n=1,则( )
,其中m+n=1,则( )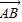 与
与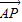 的方向一定相同
的方向一定相同