题目内容
（08年龙岩一中冲刺文）（14分）
如图，在矩形
中，
，
，
、
分别是边
、
的中点，
在所在直线上移动，
的垂直平分线
交直线
于点
，点
满足关系式
．
（1）建立适当的直角坐标系，求点的轨迹
的方程；
（2）过点作互相垂直的直线
、
，分别交曲线于
、
和
、
，求四边形
面积的最小值．
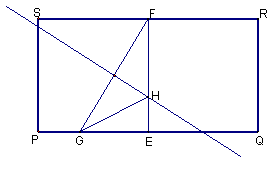
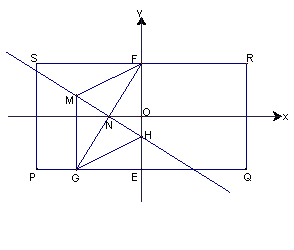
解析：（1）以线段
的中点为坐标原点，所在直线为
轴建立平面直角坐标系，当点
与点
不重合时，
，∴四边形
为平行四边形，
是
的垂直平分线，
，
因此平行四边形为菱形，即
在直线
上，
∥
， ……………2分
又
，于是动点
到定点
的距离与到定直线
的距离相等，故动点
的轨迹为抛物线．由于点到直线的距离等于
，于是
，
从而点的轨迹方程为
……………4分
当点与点重合时，
，
、重合于的中点
故动点的轨迹
的方程是
……………6分
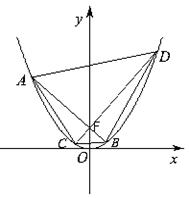
（2）依题意，直线
的斜率存在且不为
，设直线
的方程为
，
由
得
的方程为
，将代入
，
化简得
……………………8分
设
则
…………10分
同理可得
…………………11分
∴四边形
的面积
当且仅当 
即
时，
故四边形面积的最小值是
…………………14分
练习册系列答案
相关题目
和
（其中
），
，
．
的取值范围；
有几个实根？为什么？
中，
，
，
是
的中点，将
沿
折起，使点
折到点
的位置，且二面角
的大小为
与平面
所成角的大小
到平面
的距离
的两个焦点为
，
，
为动点，若
，
为定值（其中
的最小值为
.
的方程；
，过点
作直线
交轨迹
，
两点，判断
的大小是否为定值？并证明你的结论.
简记为
，若由
构成的数列
满足
其中
是y轴正方向相同的单位向量，则
是否为T点列，并说明理由；
在
的右上方，任取其中连续三点
，判定
的形状（锐角三角形、直角三角形、钝角三角形），并予以证明；
满足
.求证：
， 
，求
的单调递增区间； 
的定义域为
，值域为[2，5]，求a，b的值.