题目内容
给出两个函数性质:
性质1: 是偶函数;
是偶函数;
性质2: 在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
对于函数:① ;②
;② ; ③
; ③ ,
,
上述两个函数性质都具有的所有函数的序号是 .
②
【解析】
试题分析对于①f(x)=|x+2|,f(x+2)=|x+4|关于直线x=﹣4对称,不满足性质1,故不正确;
对于②f(x)=(x﹣2)2,f(x+2)=x2,是偶函数,f(x)=(x﹣2)2,关于直线x=2对称,且在(﹣∞,2)上是减函数,在(2,+∞)上是增函数,故满足两个函数性质;
对于③f(x)=cos(x﹣2),f(x+2)=cosx,是偶函数,但f(x)=cos(x﹣2),不满足在(﹣∞,2)上是减函数,在(2,+∞)上是增函数,故不正确.
考点:函数奇偶性及图象变化.

练习册系列答案
相关题目
 .对
.对 ,该数列前
,该数列前 项的最大值记为
项的最大值记为 ,后
,后 项
项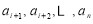 的最小值记为
的最小值记为 ,
, .
. 为
为 ,写出
,写出 ,
, ,
, 的值;
的值; (
( )是公比大于
)是公比大于 的等比数列,且
的等比数列,且 .证明:
.证明: 是等比数列;
是等比数列; 是公差大于
是公差大于 的等差数列,且
的等差数列,且 .证明:
.证明: 是等差数列.
是等差数列. ,其中
,其中 ,且
,且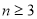 ,若对
,若对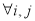 (
(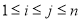 ),
),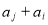 与
与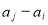 两数中至少有一个属于
两数中至少有一个属于 ,则称数集
,则称数集 具有性质
具有性质
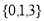 与数集
与数集 是否具有性质
是否具有性质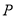 ,说明理由
,说明理由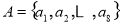 具有性质
具有性质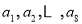 是否为等差数列,若是等差数列,请证明;若不是,请说明理由
是否为等差数列,若是等差数列,请证明;若不是,请说明理由 q为真命题,则p
q为真命题,则p q为真命题。
q为真命题。 ”是“
”是“ ”的充分不必要条件。
”的充分不必要条件。 x∈R,使得x
x∈R,使得x +x-1<0,则
+x-1<0,则 p :
p : x∈R,使得x
x∈R,使得x ,则x=1或x=2”的逆否命题为“若x
,则x=1或x=2”的逆否命题为“若x 1或x
1或x 2,则
2,则 ”。
”。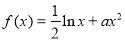
 .
.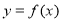 在点
在点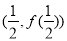 处的切线
处的切线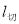 与直线
与直线 :
: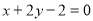 垂直,求
垂直,求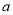 的值;
的值;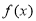 的单调性;若存在极值点
的单调性;若存在极值点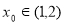 ,求实数
,求实数 的取值范围.
的取值范围. 为不等式组
为不等式组 ,表示的平面区域上的一点,则
,表示的平面区域上的一点,则 的取值范围为
的取值范围为 B.
B. C.
C. D.
D.
 的值为
的值为 B.
B. C.
C. D.
D.
 的前
的前 项和记为
项和记为 ,已知
,已知 ,求
,求 ______________.
______________.