题目内容
如图,已知四棱锥 ,底面
,底面 是等腰梯形,
是等腰梯形,
且 ∥
∥ ,
, 是
是 中点,
中点, 平面
平面 ,
,
 ,
, 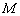 是
是 中点.
中点.
(1)证明:平面 平面
平面 ;
;
(2)求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(1) 证明:
 且
且 ∥
∥ ,
,
则 平行且等于
平行且等于 ,即四边形
,即四边形 为平行四边形,所以
为平行四边形,所以 .
.


(2) 『解法1』:
延长 、
、 交于点
交于点 ,连结
,连结 ,则
,则
 平面
平面
 ,易证△
,易证△ 与△
与△ 全等,过
全等,过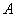 作
作 于
于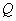 ,连
,连 ,则
,则 ,由二面角定义可知,平面角
,由二面角定义可知,平面角 为所求角或其补角.
为所求角或其补角.
易求 ,又
,又 ,
, ,由面积桥求得
,由面积桥求得 ,所以
,所以

所以所求角为 ,所以
,所以
因此平面 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为
『解法2』:
以 为原点,
为原点, 方向为
方向为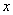 轴,以平面
轴,以平面 内过
内过 点且垂直于
点且垂直于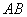 方向为
方向为 轴 以
轴 以 方向为
方向为 轴,建立如图所示空间直角坐标系.
轴,建立如图所示空间直角坐标系.
则 ,
, ,
, ,
,

 ,
,
所以 ,
, ,
,
可求得平面 的法向量为
的法向量为
又 ,
, ,
,
可求得平面 的法向量为
的法向量为
则 ,
,
因此平面 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为 .
.

练习册系列答案
相关题目
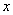 的不等式
的不等式 有且仅有三个整数解,则实数
有且仅有三个整数解,则实数 的取值范围为
的取值范围为  的解集为(-1,2),则
的解集为(-1,2),则 。
。 和直线
和直线 ,抛物线
,抛物线 上一动点
上一动点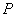 到直线
到直线
 的距离之和的最小值是
的距离之和的最小值是 B.2 C.
B.2 C. D.3
D.3 的展开式的常数项为
的展开式的常数项为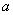 ,则直线
,则直线 与曲线
与曲线 围成图形的面积为 .
围成图形的面积为 .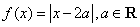 .
.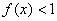 的解集为
的解集为 ,求
,求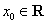 ,使
,使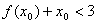 ,求
,求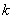 值是
值是 
 .若
.若 ,则
,则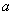 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.

 在
在 上的最小值;
上的最小值;  恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;