题目内容
已知
(1)求函数f(x)的定义域和值域;
(2)若函数 ,求函数F(x)的最大值和最小值.
,求函数F(x)的最大值和最小值.
解:(1)由 得
得 ,…
,…
故定义域为[-3,1]…
由 得:
得:

从而 ,…
,…
故值域为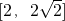 …
…
(2)令f(x)=t,
下证明:函数 正区间
正区间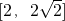 上单调递增
上单调递增
y'=1-
当t∈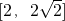 时,y′>0
时,y′>0
∴函数 正区间
正区间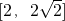 上单调递增
上单调递增
从而 …
…
 …
…
分析:(1)根据偶次根式下大于等于0建立不等式组,解之即可求出定义域,将函数平方,利用二次函数的性质可求出该函数的值域;
(2)利用换元法,f(x)=t, ,则
,则 ,然后利用导数证明该函数的单调性,可求出函数的最值.
,然后利用导数证明该函数的单调性,可求出函数的最值.
点评:本题主要考查了函数定义域和值域,以及利用导数研究函数的单调性求最值,同时考查了计算能力,属于中档题.
 得
得 ,…
,…故定义域为[-3,1]…
由
 得:
得:
从而
 ,…
,…故值域为
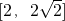 …
…(2)令f(x)=t,

下证明:函数
 正区间
正区间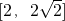 上单调递增
上单调递增y'=1-

当t∈
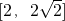 时,y′>0
时,y′>0∴函数
 正区间
正区间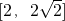 上单调递增
上单调递增从而
 …
… …
…分析:(1)根据偶次根式下大于等于0建立不等式组,解之即可求出定义域,将函数平方,利用二次函数的性质可求出该函数的值域;
(2)利用换元法,f(x)=t,
 ,则
,则 ,然后利用导数证明该函数的单调性,可求出函数的最值.
,然后利用导数证明该函数的单调性,可求出函数的最值.点评:本题主要考查了函数定义域和值域,以及利用导数研究函数的单调性求最值,同时考查了计算能力,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目



 上的值域。
上的值域。

 ,若不等式f(a1)+f(a2)+f(a3)+…+f(a2009)≤x-ln(x-p)在x∈(p,+∞)时恒成立,求实数p的最小值.
,若不等式f(a1)+f(a2)+f(a3)+…+f(a2009)≤x-ln(x-p)在x∈(p,+∞)时恒成立,求实数p的最小值.