题目内容
矩形ABCD的长AB=8,宽AD=5,动点E、F分别在边BC、CD上,且CE=CF=x,将△AEF的面积S表示为x的函数f(x).
(1)求函数S=f(x)的解析式及定义域;
(2)求S的值域.
(1)求函数S=f(x)的解析式及定义域;
(2)求S的值域.
(1)S=f(x)=S平行四边形ABCD-S△CEF-S△ABE-S△ADF
=40-
x2-
×8×(5-x)-
×5×(8-x)
=-
x2+
x
=-
(x-
)2+
.
∵CE≤CB≤CD,∴0<x≤5,
∴函数S=f(x)的解析式:S=f(x)=-
(x-
)2+
(0<x≤5);
定义域(0,5];
(2)∵f(x)在x∈(0,5]上单调递增,∴Smax=f(5)=20,
即S的最大值为20.
∴值域(0,20].
=40-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 13 |
| 2 |
=-
| 1 |
| 2 |
| 13 |
| 2 |
| 169 |
| 8 |
∵CE≤CB≤CD,∴0<x≤5,
∴函数S=f(x)的解析式:S=f(x)=-
| 1 |
| 2 |
| 13 |
| 2 |
| 169 |
| 8 |
定义域(0,5];
(2)∵f(x)在x∈(0,5]上单调递增,∴Smax=f(5)=20,
即S的最大值为20.
∴值域(0,20].

练习册系列答案
相关题目
 如图,矩形ABCD的长AB=2,宽AD=x,若PA⊥平面ABCD,矩形的边CD上至少有一个点Q,使得PQ⊥BQ,则x的范围是( )
如图,矩形ABCD的长AB=2,宽AD=x,若PA⊥平面ABCD,矩形的边CD上至少有一个点Q,使得PQ⊥BQ,则x的范围是( )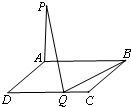 如图,矩形ABCD的长AB=2,宽AD=x,若PA⊥平面ABCD,矩形的边CD上至少有一个点Q,使得PQ⊥BQ,则x的范围是
如图,矩形ABCD的长AB=2,宽AD=x,若PA⊥平面ABCD,矩形的边CD上至少有一个点Q,使得PQ⊥BQ,则x的范围是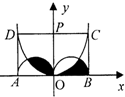 如图,矩形ABCD的长AB=6cm,宽AD=3cm.O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.抛物线y=ax2经过C、D两点,则图中阴影部分的面积是
如图,矩形ABCD的长AB=6cm,宽AD=3cm.O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.抛物线y=ax2经过C、D两点,则图中阴影部分的面积是