题目内容
设函数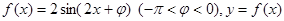 图像的一条对称轴是直线
图像的一条对称轴是直线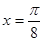 .
.
(1)求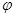 ;
;
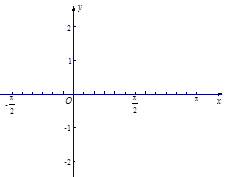
(2)画出函数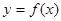 在区间
在区间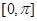 上的图像.
上的图像.
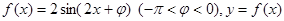 图像的一条对称轴是直线
图像的一条对称轴是直线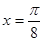 .
.
(1)求
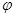 ;
;(2)画出函数
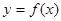 在区间
在区间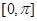 上的图像.
上的图像.(1) ;
;
(2)图像如图(正确得8分,错误酌情减分)

 ;
;(2)图像如图(正确得8分,错误酌情减分)

试题分析:(1)由题意知x=
 是函数
是函数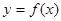 图像的一条对称轴,
图像的一条对称轴,所以
 ,
, ,
, 4分
4分(2)由(1)得,
 ,其草图如图(正确得8分,错误酌情减分)
,其草图如图(正确得8分,错误酌情减分)
点评:中档题,此类问题,一般先观察图象确定A,T,利用代入点的坐标求
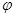 。画图可以利用“五点法”。
。画图可以利用“五点法”。
练习册系列答案
相关题目
 一个周期内的图象如图,其中
一个周期内的图象如图,其中 ,且
,且 两点在
两点在 轴两侧,则下列区间是
轴两侧,则下列区间是 的单调区间的是 ( )
的单调区间的是 ( )





 内的单调递增区间;
内的单调递增区间; 内的值域.
内的值域. 的图形按向量
的图形按向量 平移后得到函数
平移后得到函数 的图形,满足
的图形,满足 ,则向量
,则向量 的一个可能值是( )
的一个可能值是( )



 的最小正周期为
的最小正周期为 ,为了得到函数
,为了得到函数 的图像,只要将
的图像,只要将 的图像( )
的图像( ) 个单位长度
个单位长度 个单位长度
个单位长度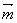 =(
=(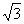 sin2x+2,cosx),
sin2x+2,cosx),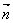 =(1,2cosx),设函数f(x)=
=(1,2cosx),设函数f(x)=  ,
, R.
R. (
( ,
, 的单调递减区间;
的单调递减区间; 时,求函数
时,求函数 .
. .
. 的最小正周期和值域;
的最小正周期和值域; 为第二象限角,且
为第二象限角,且 ,求
,求 的值.
的值.