题目内容
解不等式：
≥2.
解：原不等式可化为-2≥0，
即
≥0.
因分子、分母必须同号，
则又可化为
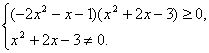
由于-2x2-x-1恒为负值，不等式除以（-2x2-x-1）得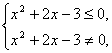
即x2+2x-3＜0,则（x+3）(x-1)＜0,解得-3＜x＜1.
所以原不等式的解集为{x|-3＜x＜1}.
练习册系列答案
相关题目
≥2.题目内容
解不等式：≥2.
解：原不等式可化为-2≥0，
即≥0.
因分子、分母必须同号，
则又可化为
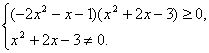
由于-2x2-x-1恒为负值，不等式除以（-2x2-x-1）得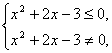
即x2+2x-3＜0,则（x+3）(x-1)＜0,解得-3＜x＜1.
所以原不等式的解集为{x|-3＜x＜1}.