题目内容
已知a1,a2,…,a8是首项为1,公比为2的等比数列,对于1≤k<8的整数k,数列b1,b2,…,b8由bn=
确定.记C=
anbn.
(I)求k=3时C的值(求出具体的数值);
(Ⅱ)求C最小时k的值.
|
| 8 |
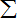 |
| n=1 |
(I)求k=3时C的值(求出具体的数值);
(Ⅱ)求C最小时k的值.
(I)显然an=2n-1(1≤n≤8).
∴k=3,∴bn=
∴C=
anbn=
anan+3+
anan-5=
22n+1+
22n-6
=(23+25+27+29+211)+(25+27+29)
=3400.
(II)∵bn=
∴C=
anbn=
anan+k+
anan+k-8=
22n+k-2+
22n+k-10,
=
+
=
(216-k-2k+28+k-28-k)
=
(212-24)(24-k+2k-4)≥
(212-24)
=2720.
∴当且仅当24-k=2k-4时,C的值最小,此时解得k=4.
∴k=3,∴bn=
|
∴C=
| 8 |
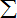 |
| n=1 |
| 5 |
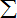 |
| n=1 |
| 8 |
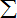 |
| n=6 |
| 5 |
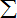 |
| n=1 |
| 8 |
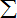 |
| n=6 |
=(23+25+27+29+211)+(25+27+29)
=3400.
(II)∵bn=
|
∴C=
| 8 |
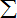 |
| n=1 |
| 8-k |
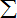 |
| n=1 |
| 8 |
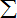 |
| n=0-k |
| 8-k |
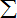 |
| n=1 |
| 8 |
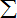 |
| n=9-k |
=
| 2k(48-k-1) |
| 4-1 |
| 28-k(4k-1) |
| 4-1 |
| 1 |
| 3 |
=
| 1 |
| 3 |
| 2 |
| 3 |
| 24-k•2k-4 |
∴当且仅当24-k=2k-4时,C的值最小,此时解得k=4.

练习册系列答案
相关题目
已知
,
均为单位向量,那么
=(
,
)是
+
=(
,1)的( )
| a1 |
| a2 |
| a1 |
| ||
| 2 |
| 1 |
| 2 |
| a1 |
| a2 |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |