题目内容
(本题满分共13分)已知正项数列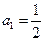 ,函数
,函数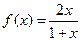 。(1)若正项数列
。(1)若正项数列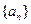 满足
满足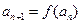 (
(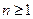 且
且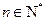 ),试求出
),试求出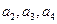 由此归纳出通项
由此归纳出通项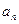 ,并证明之;(2)若正项数列
,并证明之;(2)若正项数列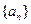 满足
满足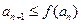 (
(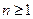 且
且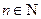 ),数列
),数列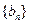 满足
满足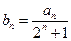 ,其和为
,其和为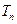 ,求证
,求证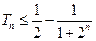 。
。
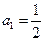 ,函数
,函数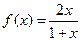 。(1)若正项数列
。(1)若正项数列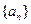 满足
满足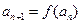 (
(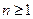 且
且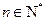 ),试求出
),试求出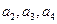 由此归纳出通项
由此归纳出通项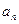 ,并证明之;(2)若正项数列
,并证明之;(2)若正项数列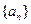 满足
满足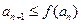 (
(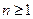 且
且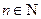 ),数列
),数列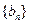 满足
满足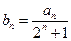 ,其和为
,其和为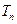 ,求证
,求证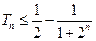 。
。(Ⅰ)略(Ⅱ) 略
:(1) ,
, ,
, 归纳出
归纳出 …
…
证明:由



 是以
是以 为首项,
为首项, 为公比等比数列
为公比等比数列


 故通项
故通项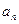 是正确的。 ……
是正确的。 ……
(2)由 得
得
 故
故 ,
,
累乘
 即
即 故
故




故 ……13分
……13分
 ,
, ,
, 归纳出
归纳出 …
…
证明:由




 是以
是以 为首项,
为首项, 为公比等比数列
为公比等比数列

 故通项
故通项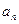 是正确的。 ……
是正确的。 ……
(2)由
 得
得
 故
故 ,
,
累乘

 即
即 故
故




故
 ……13分
……13分
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
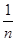 ),f(
),f(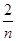 ),
),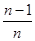 )……,(n≥2,n∈
)……,(n≥2,n∈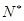 )的前n项的和为Sn ;
)的前n项的和为Sn ;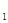 =
=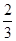 ,a
,a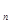 =" "
=" " 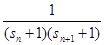 (n≥2,n∈
(n≥2,n∈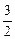 ,a3=f(x).
,a3=f(x). 已知函数
已知函数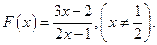
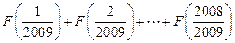 ;(2)已知数列
;(2)已知数列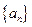 满足
满足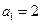 ,
,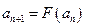 ,求数列
,求数列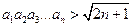 .
.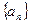 的公差为2,若
的公差为2,若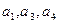 成等比数列, 则
成等比数列, 则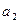 =" ( " )
=" ( " )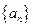 是等差数列,若
是等差数列,若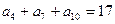 ,
,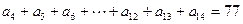 且
且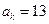 ,则
,则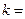 ___
___ 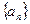 是递增等差数列,前三项的和为12,前三项的积为48,则它的公差为( )
是递增等差数列,前三项的和为12,前三项的积为48,则它的公差为( )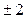
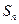 是等差数列
是等差数列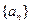 的前
的前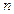 项和,若
项和,若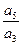 =
=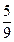 ,则
,则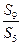 等于
等于