题目内容
椭圆的焦点是F1（-3，0）F2（3，0），P为椭圆上一点，且|F1F2|是|PF1|与|PF2|的等差中项，则椭圆的方程为________．
分析：根据椭圆和数列的基本性质以及题中已知条件便可求出a和b值，进而求得椭圆方程．
解答：∵椭圆的焦点是F1（-3，0）F2（3，0），
P为椭圆上一点，且|F1F2|是|PF1|与|PF2|的等差中项，
∴|PF1|+|PF2|=2|F1F2|=12，
∴2a=12，2c=6，即a=6，c=3
∴b2=36-9=27，
∴椭圆的方程为
．故答案为：
．点评：本题椭圆标准方程的求解利用了椭圆的定义，关键是求出其基本量，体现了转化化归的数学思想．
练习册系列答案
阅读快车系列答案
相关题目
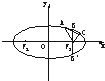已知某椭圆的焦点是F1（-4，0）、F2（4，0），过点F2，并垂直于x轴的直线与椭圆的一个交点为B，且|F1B|+|F2B|=10．椭圆上不同的两点A（x1，y1）、C（x2，y2）满足条件：|F2A|、|F2B|、|F2C|成等差数列．
已知某椭圆的焦点是F1（-4，0）、F2（4，0），过点F2并垂直于x轴的直线与椭圆的一个交点为B，且|F1B|+|F2B|=10，椭圆上不同的两点A（x1，y1）、C（x2，y2）满足条件：|F2A|、|F2B|、|F2C|成等差数列．