Question

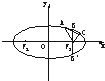已知某椭圆的焦点是F₁（-4，0）、F₂（4，0），过点F₂，并垂直于x轴的直线与椭圆的一个交点为B，且|F₁B|+|F₂B|=10．椭圆上不同的两点A（x₁，y₁）、C（x₂，y₂）满足条件：|F₂A|、|F₂B|、|F₂C|成等差数列．
（1）求该椭圆的方程；
（2）求弦AC中点的横坐标；
（3）设弦AC的垂直平分线的方程为y=kx+m，求m的取值范围．

Answer 1

分析：（1）由椭圆定义及条件知2a=|F₁B|+|F₂B|=10，得a=5．又c=4，所以b=

a2-c2

=3．由此可知椭圆方程为

x2

25

+

y2

9

=1．
（2）由点B（4，y_B）在椭圆上，得|F₂B|=|y_B|=

9

5

．因为椭圆右准线方程为x=

25

4

，离心率为

4

5

．根据椭圆定义，有|F₂A|=

4

5

（

25

4

-x₁），|F₂C|=

4

5

（

25

4

-x₂）．由|F₂A|、|F₂B|、|F₂C|成等差数列，得x₁+x₂=8．由此可知x₀=

x1+x2

2

=

8

2

=4．
（3）由A（x₁，y₁），C（x₂，y₂）在椭圆上，得9（

x1+x2

2

）+25（

y1+y2

2

）（

y1-y2

x1-x2

）=0（x₁≠x₂）．将

x1+x2

2

=x₀=4，

y1+y2

2

=y₀，

y1-y2

x1-x2

=-

1

k

（k≠0）代入上式，得9×4+25y₀（-

1

k

）=0（k≠0）．由此可求出m的取值范围．

解答：（1）解：由椭圆定义及条件知
2a=|F₁B|+|F₂B|=10，得a=5．又c=4，
所以b=

a2-c2

=3．
故椭圆方程为

x2

25

+

y2

9

=1．
（2）解：由点B（4，y_B）在椭圆上，得|F₂B|=|y_B|=

9

5

．
因为椭圆右准线方程为x=

25

4

，离心率为

4

5

．
根据椭圆定义，有|F₂A|=

4

5

（

25

4

-x₁），|F₂C|=

4

5

（

25

4

-x₂）．
由|F₂A|、|F₂B|、|F₂C|成等差数列，得

4

5

（

25

4

-x₁）+

4

5

（

25

4

-x₂）=2×

9

5

．
由此得出x₁+x₂=8．
设弦AC的中点为P（x₀，y₀），
则x₀=

x1+x2

2

=

8

2

=4．
（3）解：由A（x₁，y₁），C（x₂，y₂）在椭圆上，得
9x₁²+25y₁²=9×25，④
9x₂²+25y₂²=9×25．⑤
由④-⑤得9（x₁²-x₂²）+25（y₁²-y₂²）=0，
即9（

x1+x2

2

）+25（

y1+y2

2

）（

y1-y2

x1-x2

）=0（x₁≠x₂）．
将

x1+x2

2

=x₀=4，

y1+y2

2

=y₀，

y1-y2

x1-x2

=-

1

k

（k≠0）代入上式，得
9×4+25y₀（-

1

k

）=0（k≠0）．
由上式得k=

25

36

y₀（当k=0时也成立）．
由点P（4，y₀）在弦AC的垂直平分线上，得
y₀=4k+m，
所以m=y₀-4k=y₀-

25

9

y₀=-

16

9

y₀．
由P（4，y₀）在线段BB′（B′与B关于x轴对称）的内部，得-

9

5

＜y₀＜

9

5

．
所以-

16

5

＜m＜

16

5

．

点评：在推导过程中，未写明“x₁≠x₂”“k≠0”“k=0时也成立”及把结论写为“-

16

5

≤m≤

16

5

”也可以．