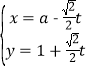Question

【题目】已知函数，，若对任意给定的，关于的方程在区间上总存在唯一的一个解，则实数的取值范围是（ ）

A. B. C. D.

Answer 1

【答案】B

【解析】分析：由题意可以把问题转化为求函数f（x）和函数g（x）的值域，并有题意转化为两个函数的值域的关系问题．

详解：解f′（x）=6ax2﹣6ax=6ax（x﹣1），

①当a=0时，f（x）=1，g（x）=，显然不可能满足题意；

②当a＞0时，f'（x）=6ax2﹣6ax=6ax（x﹣1），

x，f′（x），f（x）的变化如下：

又因为当a＞0时，g（x）=﹣x+上是减函数，

对任意m∈[0，2]，g（m）∈[﹣+，]，

由题意，必有g（m）max≤f（x）max，且1﹣a＞0，

故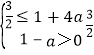，解得：≤a＜1，

③当a＜0时，g（x）=﹣x+上是增函数，不合题意；

综上，a∈[，1），

故选：B．