题目内容
在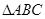 中,角
中,角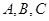 的对边分别是
的对边分别是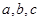 ,下列命题:
,下列命题:
①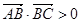 ,则△ABC为钝角三角形。
,则△ABC为钝角三角形。
②若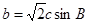 ,则C=45º.
,则C=45º.
③若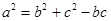 ,则
,则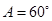 .
.
④若已知E为△ABC的边BC的中点,△ABC所在平面内有一点P,满足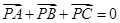 ,设
,设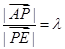 ,则
,则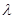 =2,其中正确命题的个数是
=2,其中正确命题的个数是
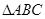 中,角
中,角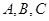 的对边分别是
的对边分别是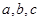 ,下列命题:
,下列命题:①
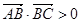 ,则△ABC为钝角三角形。
,则△ABC为钝角三角形。②若
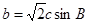 ,则C=45º.
,则C=45º.③若
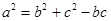 ,则
,则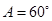 .
.④若已知E为△ABC的边BC的中点,△ABC所在平面内有一点P,满足
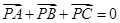 ,设
,设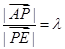 ,则
,则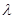 =2,其中正确命题的个数是
=2,其中正确命题的个数是| A.1 | B.2 | C.3 | D.4 |
C
专题:综合题.
分析:利用向量的数量积公式及向量夹角与三角形内角的关系,判断出①的对错;
利用正弦定理判断出②的对错;
利用余弦定理判断出③的对错;
利用三角形重心满足的向量关系及重心的度量关系判断出④的对错.
解答:解:对于①,∵
 >0所以两个向量的夹角为锐角,又两个向量的夹角为三角形的内角B的补角,所以B为钝角,所以△ABC为钝角三角形,故①对
>0所以两个向量的夹角为锐角,又两个向量的夹角为三角形的内角B的补角,所以B为钝角,所以△ABC为钝角三角形,故①对对于②,由正弦定理得sinB=
 sinCsinB,所以sinC=
sinCsinB,所以sinC= ,所以C=45°或135°,故②错
,所以C=45°或135°,故②错对于③,由三角形中的余弦定理,得b2+c2-2bccosA=b2+c2-bc即cosA=
 则A=60°,故③对
则A=60°,故③对对于④,∵
 +
+ +
+ =0∴P为三角形的重心,所以
=0∴P为三角形的重心,所以 =2,∴λ=2,故④对.
=2,∴λ=2,故④对.故选C
点评:在三角形中,当条件中出现边的平方关系或角的余弦形式时常利用余弦定理解决;当条件中出现正弦形式时常考虑正弦定理解决;三角形的重心满足的向量关系:以重心为始点,三角形的三顶点为终点对应的三向量和为零向量.

练习册系列答案
相关题目
 中,如果
中,如果
 则
则 的大小是 ( )
的大小是 ( )

 或
或
 的零点个数是 ( )
的零点个数是 ( )
 中,已知
中,已知 顶点
顶点 和
和 ,顶点
,顶点 在椭圆
在椭圆 上,则
上,则 的值是
的值是  中,
中, ,
, ,则角
,则角 等于
等于



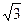 ,bc=48,b-c=2,
,bc=48,b-c=2,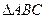 中,
中,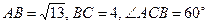 ,则
,则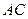 的长等于__________________.
的长等于__________________. 、
、 、
、 ,则此人( )
,则此人( )