题目内容
将两块三角板按图甲方式拼好(A、B、C、D四点共面),其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使点D在平面ABC上的射影O恰好在AB上(如图乙)。
(1)求证:AD⊥平面BDC;
(2)求二面角D-AC-B的大小;
(3)求异面直线AC与BD所成角的大小。
(1)求证:AD⊥平面BDC;
(2)求二面角D-AC-B的大小;
(3)求异面直线AC与BD所成角的大小。

(1)证明:由已知DO⊥平面ABC,
∴平面ADB⊥平面ABC,
又∵BC⊥AB,
∴BC⊥平面ADB,
又∵AD 平面ADB,
平面ADB,
∴BC⊥AD,
又∵AD⊥DC,
∴AD⊥平面BDC。
(2)解:由(1)得AD⊥BD,由已知AC=2,得 ,AD=1,
,AD=1,
∴BD=1,∴O是AB的中点, ,
,
过D作DE⊥AC于E,连结OE,则OE⊥AC,
∴∠DEO是二面角D-AC-B的平面角,且 ,
,
∴ ,
,
即二面角D-AC-B的大小为 .
.
(3)解:取AC的中点G,连结OG,
以O为原点,分别以GO、OB、OD所在直线为x轴、y轴、z轴,建立空间直角坐标系,
则 ,
, ,
,
∴ ,
,
设AC与BD所成的角为α,则 ,∴α=60°,
,∴α=60°,
即异面直线AC与BD所成角的大小为60°。
∴平面ADB⊥平面ABC,
又∵BC⊥AB,
∴BC⊥平面ADB,
又∵AD
 平面ADB,
平面ADB,∴BC⊥AD,
又∵AD⊥DC,
∴AD⊥平面BDC。
(2)解:由(1)得AD⊥BD,由已知AC=2,得
 ,AD=1,
,AD=1,∴BD=1,∴O是AB的中点,
 ,
,过D作DE⊥AC于E,连结OE,则OE⊥AC,
∴∠DEO是二面角D-AC-B的平面角,且
 ,
,∴
 ,
,即二面角D-AC-B的大小为
 .
. (3)解:取AC的中点G,连结OG,
以O为原点,分别以GO、OB、OD所在直线为x轴、y轴、z轴,建立空间直角坐标系,
则
 ,
, ,
,∴
 ,
,设AC与BD所成的角为α,则
 ,∴α=60°,
,∴α=60°,即异面直线AC与BD所成角的大小为60°。

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
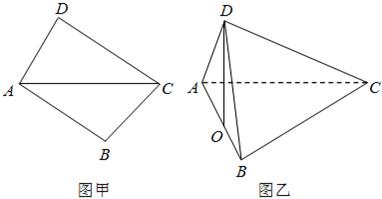 将两块三角板按图甲方式拼好,其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.
将两块三角板按图甲方式拼好,其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.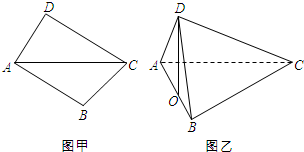 将两块三角板按图甲方式拼好(A、B、C、D四点共面),其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使点D在平面ABC上的射影O恰好在AB上(如图乙).
将两块三角板按图甲方式拼好(A、B、C、D四点共面),其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使点D在平面ABC上的射影O恰好在AB上(如图乙). (2008•襄阳模拟)将两块三角板按图甲方式拼好,其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.
(2008•襄阳模拟)将两块三角板按图甲方式拼好,其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙. 角板按图甲方式拼好,其中
角板按图甲方式拼好,其中 ,
, ,
, ,AC = 2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.
,AC = 2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.
 :O为线段AB中点;
:O为线段AB中点; ,
, ,
, ,
,
 ,现将三角板
,现将三角板 沿
沿 折起,使
折起,使 在平面
在平面 上的射影恰好在
上的射影恰好在 上,如图乙.
上,如图乙.
 平面
平面 ;
;
 的余弦值;
的余弦值;