题目内容
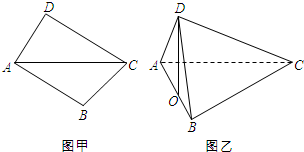 将两块三角板按图甲方式拼好(A、B、C、D四点共面),其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使点D在平面ABC上的射影O恰好在AB上(如图乙).
将两块三角板按图甲方式拼好(A、B、C、D四点共面),其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使点D在平面ABC上的射影O恰好在AB上(如图乙).(1)求证:AD⊥平面BDC;
(2)求二面角D-AC-B的大小;
(3)求异面直线AC与BD所成角的大小.
分析:(1)在平面内找两条相交直线,再分别证明这两条直线与已知直线垂直,即可利用线面垂直的判定定理得到得到线面垂直.
(2)利用题中的垂直关系作出二面角的平面角,再证明此角是所求角,然后放入三角形中利用解三角形的有关知识求解答案即可.
(3)建立空间直角坐标系,分别求出平面的法向量与直线AC所在的向量,结合向量之间的基本运算求出两个向量的夹角进而转化为线面角.
(2)利用题中的垂直关系作出二面角的平面角,再证明此角是所求角,然后放入三角形中利用解三角形的有关知识求解答案即可.
(3)建立空间直角坐标系,分别求出平面的法向量与直线AC所在的向量,结合向量之间的基本运算求出两个向量的夹角进而转化为线面角.
解答:解:(1)证明:由已知DO⊥平面ABC,
∴平面ADB⊥平面ABC,
又∵BC⊥AB,∴BC⊥平面ADB,
又∵AD?平面ADB,∴BC⊥AD,
又∵AD⊥DC,∴AD⊥平面BDC
(2)由(1)得AD⊥BD,
由已知AC=2,得AB=
,AD=1,
∴BD=1,∴O是AB的中点,DO=
过D作DE⊥AC于E,连接OE,则OE⊥AC.
∴∠DEO是二面角D-AC-B的平面角,
因为DE=
,
∴sin∠DEO=
=
.
∴∠DEO=arcsin
.
即二面角D-AC-B的大小为arcsin
.
(3)取AC的中点G,连接OG,以O为原点,分别以GO、OB、OD所在直线为x轴、y轴、z轴建立空间直角坐标系,
则A(0,-
,0),B(0,
,0),C(-
,0),D(0,0,
).
∴
=(-
,
,0),
=(0,-
,
).
设AC与BD所成的角为α,
则cosα=
=
,∴α=60°.
即异面直线AC与BD所成角的大小为60°.
(由D在平面ABC上的射影一定要落在,平面图形ABCD中,过D点与AC垂直的直线上,由平面几何知识可得O为AB中点)
∴平面ADB⊥平面ABC,
又∵BC⊥AB,∴BC⊥平面ADB,
又∵AD?平面ADB,∴BC⊥AD,
又∵AD⊥DC,∴AD⊥平面BDC
(2)由(1)得AD⊥BD,
由已知AC=2,得AB=
| 2 |
∴BD=1,∴O是AB的中点,DO=
| ||
| 2 |
过D作DE⊥AC于E,连接OE,则OE⊥AC.
∴∠DEO是二面角D-AC-B的平面角,
因为DE=
| ||
| 2 |
∴sin∠DEO=
| DO |
| DE |
| ||
| 3 |
∴∠DEO=arcsin
| ||
| 3 |
即二面角D-AC-B的大小为arcsin
| ||
| 3 |
(3)取AC的中点G,连接OG,以O为原点,分别以GO、OB、OD所在直线为x轴、y轴、z轴建立空间直角坐标系,
则A(0,-
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| AC |
| 2 |
| 2 |
| BD |
| ||
| 2 |
| ||
| 2 |
设AC与BD所成的角为α,
则cosα=
|
| ||||
|
|
| 1 |
| 2 |
即异面直线AC与BD所成角的大小为60°.
(由D在平面ABC上的射影一定要落在,平面图形ABCD中,过D点与AC垂直的直线上,由平面几何知识可得O为AB中点)
点评:夹角此类问题的关键是熟悉几何体的结构题中,不但利用题中的线面关系夹角平行、垂直、空间角等问题,也可以建立适当的坐标系借助与向量解决以上问题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
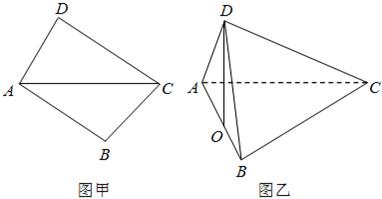 将两块三角板按图甲方式拼好,其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.
将两块三角板按图甲方式拼好,其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙. (2008•襄阳模拟)将两块三角板按图甲方式拼好,其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.
(2008•襄阳模拟)将两块三角板按图甲方式拼好,其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙. 角板按图甲方式拼好,其中
角板按图甲方式拼好,其中 ,
, ,
, ,AC = 2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.
,AC = 2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.
 :O为线段AB中点;
:O为线段AB中点; ,
, ,
, ,
,
 ,现将三角板
,现将三角板 沿
沿 折起,使
折起,使 在平面
在平面 上的射影恰好在
上的射影恰好在 上,如图乙.
上,如图乙.
 平面
平面 ;
;
 的余弦值;
的余弦值;