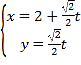题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 在
在![]() 上的单调性;
上的单调性;
(2)若![]() 有唯一零点,证明:
有唯一零点,证明:![]() .
.
【答案】(1)![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增; ![]() 时,函数
时,函数![]() 在
在![]() 上单调递减;
上单调递减;![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)见解析.
上单调递减;(2)见解析.
【解析】
(1)先求导,然后根据a的取值范围对![]() 符号的影响进行讨论,进而确定函数的单调性;
符号的影响进行讨论,进而确定函数的单调性;
(2)通过求导,求得![]() 的根
的根![]() ,函数
,函数![]() 在
在![]() 单调递减,
单调递减,![]() 单调递增,由
单调递增,由![]() 有唯一零点知,
有唯一零点知,![]() . 联立求得
. 联立求得![]() 满足的方程
满足的方程![]() ,利用导函数求出
,利用导函数求出![]() 的范围,再由
的范围,再由![]() 得出a的范围,从而命题得证.
得出a的范围,从而命题得证.
解:(1)由题意,![]() ,
,
定义域为:![]()
若![]() ,则
,则![]() 恒成立,
恒成立,
故![]() 在
在![]() 上单调递增,
上单调递增,
若![]() ,令
,令![]() ,得
,得![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() ,
,
则![]() 在
在![]() 上单调递增,
上单调递增,
②当![]() ,即
,即![]() 时,
时,![]() ,
,
则![]() 在
在![]() 上单调递减,
上单调递减,
③当![]() ,即
,即![]() 时,
时,
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
综上所述,![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,
上单调递减,
![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2)证明:由题意,![]() ,
,
![]() ,
,
令![]() ,解得
,解得![]() 是唯一的变号正根,
是唯一的变号正根,
且![]() ①
①
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
![]() ,
,
要使![]() 有唯一零点,只需
有唯一零点,只需![]() ,
,
即![]() ②
②
由①②可知,![]() ,
,
令![]() ,显然
,显然![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,
![]() ,
,
![]()
又![]()
![]()
由①知![]() ,其在
,其在![]() 上单调递增,
上单调递增,
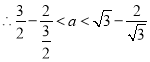
即![]() 得证.
得证.

练习册系列答案
相关题目