题目内容
如图,正方体 中,已知
中,已知 为棱
为棱 上的动点.
上的动点.
(1)求证: ;
;
(2)当 为棱
为棱 的中点时,求直线
的中点时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(1)详见解析;(2)直线 与平面
与平面 所成角的正弦是
所成角的正弦是 .
.
解析试题分析:(1)空间中证线线垂直,一般先证线面垂直.那么在本题中证哪条线垂直哪个面?从图形可看出,可证 面
面 . (2)思路一、为了求直线
. (2)思路一、为了求直线 与平面
与平面 所成角的正弦值,首先作出直线
所成角的正弦值,首先作出直线 在平面
在平面 内的射影. 连
内的射影. 连 设
设 ,连
,连 ,可证得
,可证得 面
面 ,这样
,这样 便是直线
便是直线 与平面
与平面 所成角.思路二、由于
所成角.思路二、由于 两两垂直,故可分别以
两两垂直,故可分别以 为
为 轴正向,建立空间直角坐标系,然后利用空间向量求解.
轴正向,建立空间直角坐标系,然后利用空间向量求解.
试题解析:连 设
设 ,连
,连 .
.
(1)由 面
面 ,知
,知 ,
,
又 , 故
, 故 面
面 .
.
再由 面
面 便得
便得 ⊥
⊥ .
.
(2)在正 中,
中, ,而
,而 ,
,
又 面
面 ,
, 平面
平面 ,且
,且 ,
,
故 ⊥面
⊥面 ,于是
,于是 ,
, 为二面角
为二面角 的平面角.
的平面角.
正方体ABCD— 中,设棱长为
中,设棱长为 ,且
,且 为棱
为棱 的中点,由平面几何知识易得
的中点,由平面几何知识易得 ,满足
,满足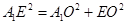 ,故
,故 .
.
再由 知
知 面
面 ,故
,故 是直线
是直线 与平面
与平面 所成角.
所成角.
又 ,故直线
,故直线 与平面
与平面 所成角的正弦是
所成角的正弦是 .
.
解二.分别以 为
为 轴正向,建立空间直角坐标系.设正方体棱长为
轴正向,建立空间直角坐标系.设正方体棱长为 .
.
(1)易得 .
.
设 ,则
,则 ,
, ,从而
,从而 ,于是
,于是
(2)由题设, ,则
,则 ,
, .
.
设
练习册系列答案
相关题目
 ,
, 为直角,
为直角, ,
, ,现以其中一直角边
,现以其中一直角边 为轴,按逆时针方向旋转
为轴,按逆时针方向旋转 后,将
后,将 点所在的位置记为
点所在的位置记为 ,再按逆时针方向继续旋转
,再按逆时针方向继续旋转 后,
后, .
. ,取
,取 ,求证:面
,求证:面 面
面 ;
; 与平面
与平面

 中,底面
中,底面 是正方形,
是正方形, ,
, ,点
,点 在
在 上,且
上,且 .
.
 平面
平面 的余弦值;
的余弦值; 上存在点
上存在点 ,使
,使 ∥平面
∥平面 ,并求
,并求 的长.
的长. 是母线
是母线 的中点,
的中点, 是底面圆的直径,底面半径
是底面圆的直径,底面半径 与母线
与母线 所成的角的大小等于
所成的角的大小等于 .
.
 时,求异面直线
时,求异面直线 与
与 所成的角;
所成的角; 的体积最大时,求
的体积最大时,求 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, 平面
平面 ,
, ,
, ,
, .
.
 平面
平面 ;
; 与平面
与平面 所成角的正切值.
所成角的正切值. 底面ABCD,
底面ABCD, ,E是PA的中点.
,E是PA的中点.
 平面EBD;
平面EBD; 中,侧面
中,侧面 ⊥底面
⊥底面 ,侧棱
,侧棱 与底面
与底面 .底面
.底面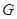 点,
点, 是线段
是线段 上一点,且
上一点,且 .
.
 //侧面
//侧面 与底面
与底面 EF=2
EF=2 ,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.
,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.