题目内容
已知平行四边形ABCD中,AC为一条对角线,若 =(2,4),
=(2,4), =(1,3),则
=(1,3),则 =( )
=( )
A. 8 8 | B. 6 6 | C.6 | D.8 |
D
解析试题分析:
=8,故选D.
考点:平面向量的坐标运算,平面向量的数量积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知直线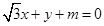 与圆
与圆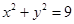 交于
交于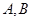 两点,则与向量
两点,则与向量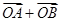 (
( 为坐标原点)共线的一个向量为( )
为坐标原点)共线的一个向量为( )
A.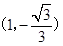 | B.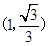 | C.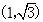 | D.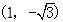 |
在平行四边形 中,若
中,若 ,则四边形
,则四边形 一定是( )
一定是( )
| A.矩形 | B.菱形 | C.正方形 | D.等腰梯形 |
设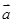 、
、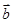 都是非零向量,下列四个条件中,一定能使
都是非零向量,下列四个条件中,一定能使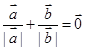 成立的是( )
成立的是( )
A.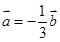 | B. | C.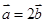 | D.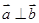 |
设点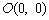 、
、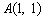 、
、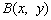 且
且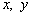 满足
满足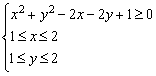 ,则
,则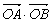 取得最小值时,点B的个数是( )
取得最小值时,点B的个数是( )
| A.1个 | B.2个 | C.3个 | D.无数个 |
如图,△ABC中,∠A=60°,∠A的平分线交BC于D,若AB=4,且 =
=
 +λ
+λ (λ∈R),则AD的长为( )
(λ∈R),则AD的长为( )
A.2 | B.3 | C.4 | D.5 |
 |=a,|
|=a,| |=b,则
|=b,则 =( )
=( )
 中,
中, ,
, 分别为
分别为 中点,
中点, 为
为 上任意一点,实数
上任意一点,实数 满足
满足 ,设
,设 的面积分别为
的面积分别为 ,
, 取得最大值时,
取得最大值时, 的值为( )
的值为( )



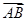 同方向的单位向量为( ).
同方向的单位向量为( ).


