题目内容
【题目】已知![]() ,其中常数
,其中常数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若函数![]() 有两个零点
有两个零点![]() ,求证:
,求证: ![]() ;
;
(3)求证: ![]() .
.
选做题:
【答案】(1) ![]() 有极小值
有极小值![]() ,没有极大值.(2)证明见解析;(3)证明见解析.
,没有极大值.(2)证明见解析;(3)证明见解析.
【解析】试题分析:先写出函数![]() 的定义域,(1)由
的定义域,(1)由![]() ,求出
,求出![]() 的导数,再求出
的导数,再求出![]() 的单调性,即可求得极值;(2)先证明:当
的单调性,即可求得极值;(2)先证明:当![]() 恒成立时,有
恒成立时,有![]() 成立,若
成立,若![]() ,则
,则![]() 显然成立;若
显然成立;若![]() ,运用参数分离,构造新函数通过求导数及单调性,结合函数零点存在定理,即可得证;(3)讨论当当
,运用参数分离,构造新函数通过求导数及单调性,结合函数零点存在定理,即可得证;(3)讨论当当![]() 时,
时, ![]() 恒成立,可设设
恒成立,可设设![]() ,求出导数,单调区间及最大值,运用不等式的性质,即可得证.
,求出导数,单调区间及最大值,运用不等式的性质,即可得证.
试题解析:函数![]() 的定义域为
的定义域为![]() ,
,
(1)当![]() 时,
时, ![]() ,
, ![]() ,
,
而![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 有极小值
有极小值![]() ,没有极大值.
,没有极大值.
(2)先证明:当![]() 恒成立时,有
恒成立时,有![]() 成立.
成立.
若![]() ,则
,则![]() 显然成立;
显然成立;
若![]() ,由
,由![]() 得
得![]() ,令
,令![]() ,
,
则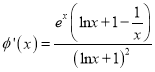 ,
,
令![]() ,由
,由![]() 得
得![]() 在
在![]() 上单调递增,
上单调递增,
又∵![]() ,所以
,所以![]() 在
在![]() 上为负,在
上为负,在![]() 上为正,
上为正,
∴![]() 在
在![]() 上递减,在
上递减,在![]() 上递增
上递增
∴![]() ,从而
,从而![]() .
.
因而函数![]() 若有两个零点,则
若有两个零点,则![]() ,所以
,所以![]() ,
,
由![]() 得
得![]() ,则
,则
![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
∴![]() 在
在![]() 上单调递增
上单调递增
∴![]() ,则
,则![]()
∴![]()
由![]() 得
得![]() ,则
,则![]()
∴![]() ,
,
综上得![]() .
.
(3)由(2)知当![]() 时,
时, ![]() 恒成立,所以
恒成立,所以![]() ,
,
即![]() ,
,
设![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递减;
上单调递减;
所以![]() 的最大值为
的最大值为![]() ,即
,即![]() ,
,
因而![]() ,
,
所以![]() ,即
,即![]()
点睛:导数是研究函数的单调性、极值(最值)最有效的工具对导数的应用的考查主要从以下几个角度进行:(1)考查导数的几何意义,往往与解析几何、微积分相联系;(2)利用导数求函数的单调区间,判断单调性;已知单调性求参数;(3)利用导数求函数的最值(极值),解决生活中的优化问题;(4)考查数形结合思想的应用.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目