题目内容
17.已知△ABC的三边长分别为a、b、c,且$\frac{a}{b}$+$\frac{a}{c}$=$\frac{b+c}{b+c-a}$,则△ABC一定是( )| A. | 等边三角形 | B. | 腰长为a的等腰三角形 | ||
| C. | 底边长为a的等腰三角形 | D. | 等腰直角三角形 |
分析 已知等式左边通分并利用同分母分式的加法法则计算,整理后根据b+c不为0得到关系式,分解因式后,利用两数相乘积为0,两因式中至少有一个为0得到a=b或a=c,即可确定出三角形形状.
解答 解:已知等式变形得:$\frac{ac+ab}{bc}=\frac{b+c}{b+c-a}$,即a(b+c)2-a2(b+c)=bc(b+c),
∵b+c≠0,∴a(b+c)-a2=bc,即ab+ac-a2-bc=0,
分解因式得:-a(a-b)+c(a-b)=0,即(a-b)(-a+c)=0,
可得a=b或a=c,
则△ABC一定为腰长为a的等腰三角形,
故选:B.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键,属于中档题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
7.若集合A={x|-2<x<1},B={x|0<x<2},则集合A∩B=( )
| A. | { x|-1<x<1} | B. | { x|-2<x<1} | C. | { x|-2<x<2} | D. | { x|0<x<1} |
8.$\int_1^2{(x-\frac{1}{x})}dx$的值是( )
| A. | 0 | B. | 1.5-ln2 | C. | 3-ln2 | D. | 1 |
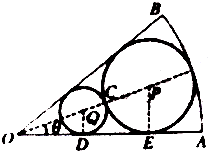 如图,在半径为1、圆心角为变量2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,设圆P的半径为R,圆Q的半径为r.
如图,在半径为1、圆心角为变量2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,设圆P的半径为R,圆Q的半径为r.