题目内容
【题目】如图,![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上异于
上异于![]() ,
,![]() 的点,直线
的点,直线![]() 平面
平面![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
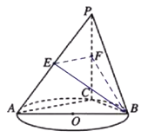
(Ⅰ)记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,试判断直线
,试判断直线![]() 与平面
与平面![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(Ⅱ)设![]() ,求二面角
,求二面角![]() 大小的取值范围.
大小的取值范围.
【答案】(Ⅰ)![]() 平面
平面![]() ,证明见解析;(Ⅱ)
,证明见解析;(Ⅱ)![]()
【解析】
(Ⅰ)证出![]() 平面
平面![]() ,由线面平行的性质定理可证出
,由线面平行的性质定理可证出![]() ,再由线面平行的判定定理即可求解.
,再由线面平行的判定定理即可求解.
(Ⅱ)法一:证出![]() 是二面角
是二面角![]() 的平面角,
的平面角,![]() ,根据
,根据![]() 的范围即可求解.
的范围即可求解.
法二:以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系,求出平面
轴建立空间直角坐标系,求出平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,利用向量的数量积即可求解.
的法向量,利用向量的数量积即可求解.
(Ⅰ)证明如下:
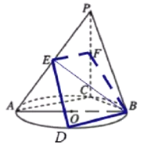
∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,平面
,平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,
,
∴![]() .
.
而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)解法一:设直线![]() 与圆
与圆![]() 的另一个交点为
的另一个交点为![]() ,连结
,连结![]() ,
,![]() .
.
由(Ⅰ)知,![]() ,而
,而![]() ,∴
,∴![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
而![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴![]() 是二面角
是二面角![]() 的平面角.
的平面角.
![]() .
.
注意到![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,
即二面角![]() 的取值范围是
的取值范围是![]() .
.
解法二:由题意,![]() ,以
,以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
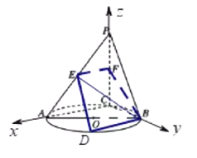
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则由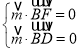 得
得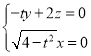 ,取
,取![]() 得
得![]() .
.
易知平面![]() 的法向量
的法向量![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,易知
,易知![]() 为锐角,
为锐角,
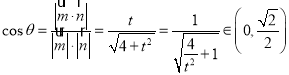 ,
,
∴![]() ,
,
即二面角![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目