题目内容
在△ABC中,内角A,B,C所对边长分别为 ,
, ,
, ,
, .
.
(1)求 的最大值及
的最大值及 的取值范围;
的取值范围;
(2)求函数 的最大值和最小值.
的最大值和最小值.
 ,
, ,
, ,
, .
.(1)求
 的最大值及
的最大值及 的取值范围;
的取值范围;(2)求函数
 的最大值和最小值.
的最大值和最小值.(Ⅰ) 的最大值为16,及
的最大值为16,及 的取值范围0<
的取值范围0<
 ;(Ⅱ)最大值为3,最小值为2.
;(Ⅱ)最大值为3,最小值为2.
 的最大值为16,及
的最大值为16,及 的取值范围0<
的取值范围0<
 ;(Ⅱ)最大值为3,最小值为2.
;(Ⅱ)最大值为3,最小值为2.试题分析:(Ⅰ)求
 的最大值及
的最大值及 的取值范围,由向量的数量积
的取值范围,由向量的数量积 ,即
,即 ,由此可想到利用余弦定理求出
,由此可想到利用余弦定理求出 ,通过基本不等式
,通过基本不等式 ,可求得b•c的最大值,再结合
,可求得b•c的最大值,再结合 ,可求出
,可求出 的取值范围;(Ⅱ)求函数
的取值范围;(Ⅱ)求函数 的最大值和最小值,可利用二倍角的正弦函数化简函数
的最大值和最小值,可利用二倍角的正弦函数化简函数 ,这样
,这样 化 为一个角的一个三角函数的形式,通过角的范围0<
化 为一个角的一个三角函数的形式,通过角的范围0<
 ,利用正弦函数的最值,从而求出函数的最大值和最小值.
,利用正弦函数的最值,从而求出函数的最大值和最小值.试题解析:(Ⅰ)

 即
即
又
 所以
所以 ,即
,即 的最大值为16
的最大值为16 即
 所以
所以  , 又0<
, 又0< <
< 所以0<
所以0<

(Ⅱ)


因0<

 ,所以
,所以 <
< ,
, 
当
 即
即 时,
时,
当
 即
即 时,
时,

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, ,函数
,函数 ,
,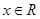 .
.
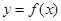 的图像的对称中心坐标;
的图像的对称中心坐标; 个单位,再向左平移
个单位,再向左平移 个单位得函数
个单位得函数 的图像,试写出
的图像,试写出 上的图像.
上的图像. sinxcosx-2cos2x+l.
sinxcosx-2cos2x+l.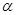 ∈(0,
∈(0, ),且f(
),且f(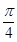 +
+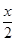 )cos(
)cos(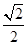 ,α∈(-
,α∈(-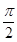 ,0),求α的值;
,0),求α的值;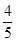 ,x∈(
,x∈(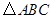 中,角
中,角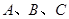 所对的边分别为
所对的边分别为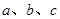 ,已知
,已知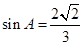 ,
,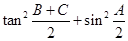 的值;
的值;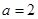 ,
,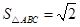 ,求
,求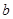 的值.
的值. .
. 的值;
的值; 的值.
的值.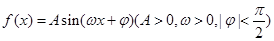 的部分图像如图示,则将
的部分图像如图示,则将 的图像向右平移
的图像向右平移 个单位后,得到的图像解析式为( )
个单位后,得到的图像解析式为( )




 的值域是 .
的值域是 . 中,已知
中,已知 ,那么
,那么