题目内容
(本小题满分12分)在三角形ABC中,内角A、B、C的对边分别为a、b、c,若 =(b,
=(b, 
 .cosB),
.cosB), =(sinA, -a),且
=(sinA, -a),且 ⊥
⊥ .
.
(1)求角B的大小;
(2)若b=3,sinC=2sinA,求△ABC的面积.
(1)B=60°;(2)
 .
.
【解析】
试题分析:(1)由两向量的坐标及两向量垂直时满足的条件列出关系式,利用正弦定理化简,整理求出tanB的值,即可确定出B的度数;
(2)利用余弦定理列出关系式,把b,cosB的值代入得到关系式,再利用正弦定理化简sinC=2sinA,得到关系式,联立求出a与c的值,再由sinB的值,利用三角形面积公式即可求出三角形ABC面积.
试题解析:(1) =(b,
=(b,  cosB)
cosB)
 =(sinA, -a)
=(sinA, -a)
 ⊥
⊥
∴b sinA- a cosB=0
a cosB=0
sinB·sinA- sinA cosB=0
sinA cosB=0
而sinA≠0
∴sinB- cosB=0
cosB=0
tanB= 又0°<B<180°
又0°<B<180°
∴B=60°
(2)b2=a2+c2-2ac cosB,b=3
∴a2+c2-ac=9 ……………………①
又∵sinC=2sinA
∴c=2a ……………………②
由①②得a= ,c=2
,c=2
∴S△ABC= ·
· ·2
·2 ·sin60°=
·sin60°=
 .
.
考点:正弦定理,余弦定理,三角形面积公式.
考点分析: 考点1:三角形的解的情况 考点2:解三角形 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的四个命题:
的四个命题: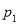 :
: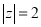 ,
, 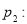
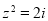
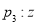 的共轭复数为
的共轭复数为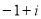
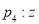 的虚部为
的虚部为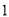
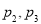 B.
B.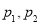 C.
C.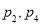 D.
D.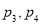
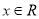 , 对于使
, 对于使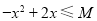 成立的所有常数
成立的所有常数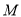 中,我们把
中,我们把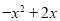 的上确界.若
的上确界.若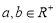 ,且
,且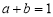 ,则
,则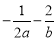 的上确界为
的上确界为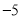 B.
B.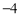 C.
C.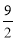 D.
D.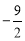
 的值域是( )
的值域是( ) B.
B. C.
C. D.
D.
 是第四象限的角,若
是第四象限的角,若 ,则
,则 ( )
( ) B.-
B.- D.-
D.-
 B.6
B.6
 D.18
D.18
 =_____.
=_____. 中,底面是边长为
中,底面是边长为 的正三角形,
的正三角形, 则直线
则直线 与侧面
与侧面 所成角的正切值为 .
所成角的正切值为 .