题目内容
已知n条直线:L1:x-y+C1=0、C1 =![]() , L2:x-y+C2=0,L3:x-y+C3=0,
, L2:x-y+C2=0,L3:x-y+C3=0,
……Ln:x-y+Cn=0 .(其中C1< C2 <C3 <……< Cn)这n条平行线中,每相邻两条之间的
距离顺次为2,3,4,……,n.
(1)求Cn ;
(2)求x-y+Cn=0与x轴、y轴围成的图形的面积;
(3)求x-y+Cn-1=0与x-y+Cn=0及x轴、y轴围成的图形的面积.(14分)
(14分)
[解析]:解:(1)由题意可知:L1到Ln的距离为:![]() =2+3+4+……+n,
=2+3+4+……+n,
∵![]() >
>![]() ∴
∴![]() =
=![]() .
.
(2)设直线Ln:x-y+cn=0交x轴于M点,交y轴于N点,则△OMN的面积为:
S△OMN=![]() │OM││ON│=
│OM││ON│=![]()
![]() =
=![]() .
.
(3)围成的图形是等腰梯形,由(2)知Sn=![]() .则有
.则有
Sn-1=![]() Sn-Sn-1=
Sn-Sn-1=![]() -
-![]() =n3 所以所求面积为n3.
=n3 所以所求面积为n3.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 且l2:x-y+C2=0,l3:x-y+C3=0,…,ln:x-y+Cn=0,其中C1<C2<C3<…<Cn,这n条平行直线中,每相邻两条之间的距离顺次为2,3,4,…,n.
且l2:x-y+C2=0,l3:x-y+C3=0,…,ln:x-y+Cn=0,其中C1<C2<C3<…<Cn,这n条平行直线中,每相邻两条之间的距离顺次为2,3,4,…,n.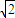 且l2:x-y+C2=0,l3:x-y+C3=0,…,ln:x-y+Cn=0,其中C1<C2<C3<…<Cn,这n条平行直线中,每相邻两条之间的距离顺次为2,3,4,…,n.
且l2:x-y+C2=0,l3:x-y+C3=0,…,ln:x-y+Cn=0,其中C1<C2<C3<…<Cn,这n条平行直线中,每相邻两条之间的距离顺次为2,3,4,…,n.