题目内容
(本小题满分13分)如图,在四棱锥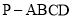 中,侧棱
中,侧棱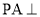 底面
底面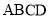 ,
,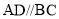 ,
,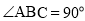 ,
,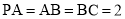 ,
,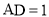 ,
,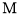 是棱
是棱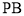 中点.
中点.
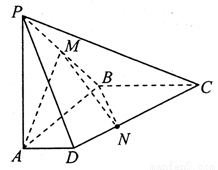
(1)求证: 平面
平面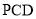 ;
;
(2)设点 是线段
是线段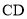 上一动点,且
上一动点,且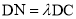 ,当直线
,当直线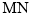 与平面
与平面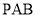 所成的角最大时,求
所成的角最大时,求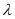 的值.
的值.
(1)利用空间向量方法证明;(2)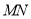 与平面
与平面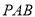 所成的角最大时
所成的角最大时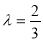 .
.
【解析】
试题分析:(1)以点A为原点建立空间直角坐标系,利用空间向量方法证明;
(2)根据点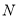 是线段
是线段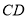 上的一点,可设
上的一点,可设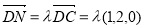 得到
得到
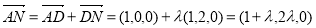
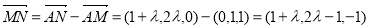
结合面PAB的法向量为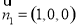 ,设
,设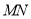 与平面
与平面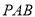 所成的角为
所成的角为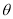 ,
,
计算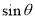 并整理得
并整理得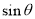
 ,根据二次函数的图象和性质即得,
,根据二次函数的图象和性质即得,
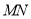 与平面
与平面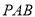 所成的角最大时
所成的角最大时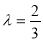 .
.
试题解析:(1)以点A为原点建立如图所示的空间直角坐标系,则
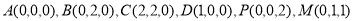
则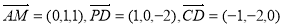

设平面PCD的法向量是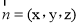 ,则
,则
 即
即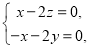
令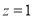 ,则
,则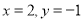 ,于是
,于是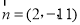
∵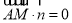 ,∴
,∴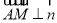 ,
,
∴AM//平面PCD 6分
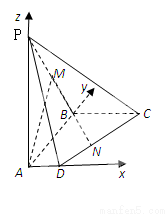
(2)因为点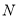 是线段
是线段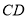 上的一点,可设
上的一点,可设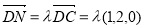
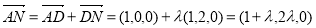
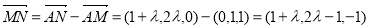
又面PAB的法向量为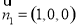
设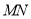 与平面
与平面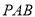 所成的角为
所成的角为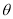
则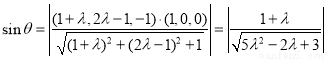



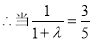 时, 即
时, 即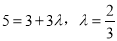 时,
时,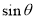 最大,
最大,
所以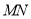 与平面
与平面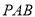 所成的角最大时
所成的角最大时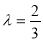 13分
13分
考点:1.空间向量方法;2.平行关系;3.空间的角.
考点分析: 考点1:点、线、面之间的位置关系 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
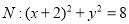 和抛物线
和抛物线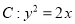 ,圆的切线
,圆的切线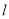 与抛物线
与抛物线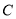 交于不同的点
交于不同的点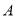 ,
, .
.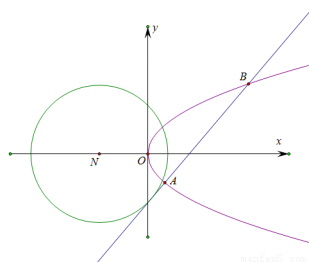
 的斜率为
的斜率为 时,求线段
时,求线段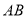 的长;
的长; 和点
和点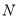 关于直线
关于直线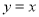 对称,问是否存在圆的切线
对称,问是否存在圆的切线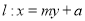 使得
使得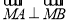 ?若存在,求出直线
?若存在,求出直线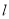 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. ,那么判断框中应填入的关于
,那么判断框中应填入的关于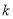 的条件是( )
的条件是( )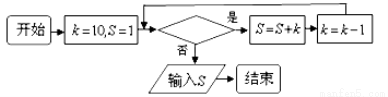
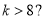 B.
B.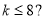 C.
C.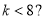 D.
D.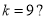
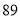
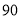
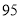
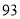
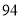
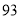
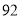 ,
,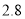 B.
B.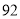 ,
,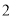 C.
C.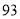 ,
,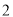 D.
D. ,
,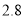
 为虚数单位,则
为虚数单位,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 中,内角
中,内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,且满足
,且满足 ,则
,则 .
.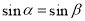 ,则
,则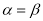 ”是真命题
”是真命题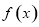 可导,且在
可导,且在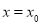 处有极值,则
处有极值,则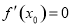
 ,
, 的夹角为钝角的充要条件是
的夹角为钝角的充要条件是
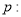 “
“ ,
,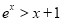 ”的否定是“
”的否定是“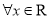 ,
,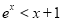 ”
” 服从正态分布
服从正态分布 . 若
. 若 ,则
,则 等于 .
等于 .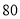 小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段
小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段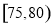 ,
,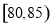 ,
,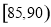 ,
,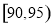 ,
,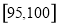 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
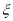 为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量
为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量 .
.