题目内容
(本小题12分)已知如图,圆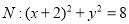 和抛物线
和抛物线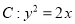 ,圆的切线
,圆的切线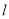 与抛物线
与抛物线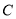 交于不同的点
交于不同的点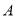 ,
, .
.
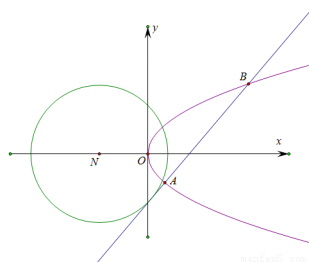
(1)当直线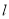 的斜率为
的斜率为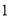 时,求线段
时,求线段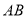 的长;
的长;
(2)设点 和点
和点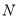 关于直线
关于直线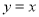 对称,问是否存在圆的切线
对称,问是否存在圆的切线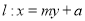 使得
使得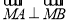 ?若存在,求出直线
?若存在,求出直线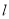 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(1)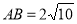 ;(2)存在,
;(2)存在,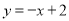 .
.
【解析】
试题分析:(1)圆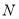 的圆心坐标为
的圆心坐标为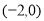 ,半径
,半径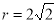 ,设
,设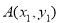 ,
,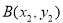 ,设
,设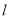 的方程,利用直线
的方程,利用直线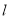 是圆
是圆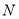 的切线,求得
的切线,求得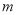 的值,从而可得直线
的值,从而可得直线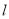 的方程,与抛物线方程联立,利用韦达定理,即可计算弦长
的方程,与抛物线方程联立,利用韦达定理,即可计算弦长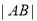 ;
;
(2)利用直线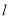 是圆
是圆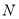 的切线,可得
的切线,可得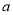 ,
,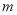 满足的一个方程,将直线
满足的一个方程,将直线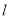 的方程与抛物线方程联立,利用
的方程与抛物线方程联立,利用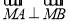 ,可得
,可得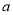 ,
,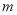 满足的另一个方程,联立方程组可求得
满足的另一个方程,联立方程组可求得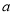 ,
,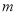 的值,从而得到满足题设的直线
的值,从而得到满足题设的直线 .
.
试题解析:∵圆 :
: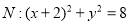 ,∴圆心坐标为
,∴圆心坐标为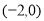 ,半径
,半径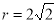 ,(1)当直线
,(1)当直线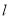 的斜率为
的斜率为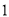 时,设
时,设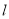 的方程为
的方程为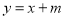 ,即
,即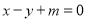 ,∵直线
,∵直线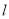 是圆
是圆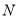 的切线,∴
的切线,∴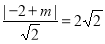 ,解得
,解得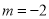 或
或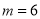 (舍),此时直线
(舍),此时直线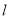 的方程为
的方程为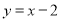 ,由
,由 ,消去
,消去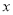 得
得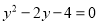 ,∴
,∴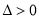 ,设
,设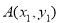 ,
,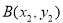 ,则
,则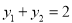 ,
,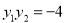 ,得
,得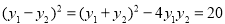 ,∴弦长
,∴弦长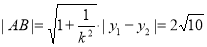 ;
;
(2)∵直线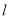 是圆
是圆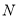 的切线,∴
的切线,∴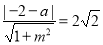 ,得
,得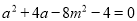 ①,由
①,由 ,消去
,消去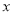 得
得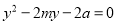 ,∴
,∴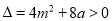 ,即
,即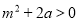 ,且
,且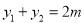 ,
,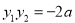 ,∵点
,∵点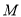 和点
和点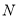 关于直线
关于直线 对称,∴点
对称,∴点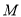 为
为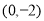 ,∴
,∴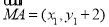 ,
,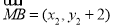 ,∵
,∵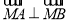 ,∴
,∴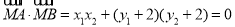 ,
,
即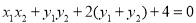 ,即
,即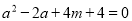 ②,①+②,得
②,①+②,得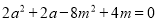 ,
,
解得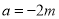 或
或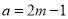 ,当
,当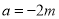 时,代入①解得
时,代入①解得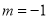 ,
,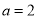 ,满足条件
,满足条件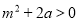 ,当
,当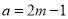 时,代入①得
时,代入①得 ,无解,综上所述,存在满足条件的直线
,无解,综上所述,存在满足条件的直线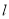 ,其方程为
,其方程为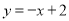 .
.
考点:1.直线与抛物线的位置关系;2.弦长的计算;3.韦达定理的运用.
考点分析: 考点1:抛物线的标准方程 考点2:抛物线的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
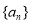 中
中
 .
.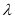 ,使数列
,使数列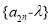 是等比数列?若存在,求
是等比数列?若存在,求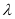 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;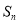 是数列
是数列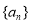 的前
的前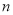 项和,求满足
项和,求满足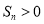 的所有正整数
的所有正整数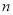 .
.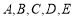 五种商品有购买意向.已知该网民购买
五种商品有购买意向.已知该网民购买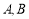 两种商品的概率均为
两种商品的概率均为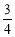 ,购买
,购买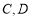 两种商品的概率均为
两种商品的概率均为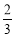 ,购买
,购买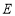 种商品的概率为
种商品的概率为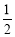 .假设该网民是否购买这五种商品相互独立.
.假设该网民是否购买这五种商品相互独立. 表示该网民购买商品的种数,求
表示该网民购买商品的种数,求 的概率分布和数学期望.
的概率分布和数学期望. 满足约束条件
满足约束条件 则目标函数
则目标函数 的最小值为 .
的最小值为 . ,
, ,则
,则 = .
= .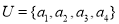 ,集合
,集合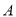 是集合
是集合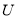 的恰有两个元素的子集,且满足下列三个条件:①若
的恰有两个元素的子集,且满足下列三个条件:①若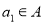 ,则
,则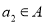 ;②若
;②若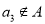 ,则
,则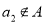 ;③若
;③若 ,则
,则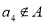 ,则集合
,则集合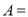 __________.(用列举法表示)
__________.(用列举法表示)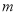 ,
,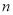 是两条不同直线,
是两条不同直线,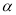 ,
, 是两个不同的平面,下列命题正确是是( )
是两个不同的平面,下列命题正确是是( ) ,
,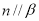 ,且
,且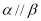 ,则
,则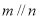
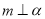 ,
,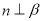 ,且
,且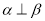 ,则
,则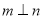
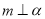 ,
,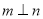 ,
,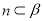 , 则
, 则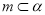 ,
,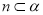 ,
,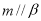 ,
,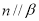 ,则
,则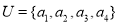 ,集合
,集合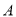 是集合
是集合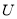 的恰有两个元素的子集,且满足下列三个条件:①若
的恰有两个元素的子集,且满足下列三个条件:①若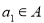 ,则
,则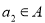 ;②若
;②若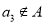 ,则
,则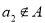 ;③若
;③若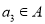 ,则
,则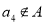 ,则集合
,则集合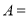 __________.(用列举法表示)
__________.(用列举法表示)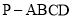 中,侧棱
中,侧棱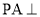 底面
底面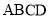 ,
,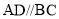 ,
,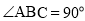 ,
,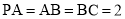 ,
,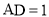 ,
,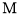 是棱
是棱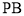 中点.
中点.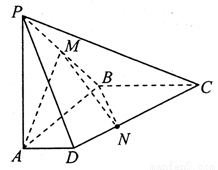
 平面
平面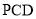 ;
; 是线段
是线段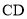 上一动点,且
上一动点,且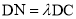 ,当直线
,当直线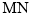 与平面
与平面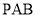 所成的角最大时,求
所成的角最大时,求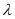 的值.
的值.