题目内容
y=(sinx-cosx)2-1是最小正周期为
- A.2π的偶函数
- B.2π的奇函数
- C.π的偶函数
- D.π的奇函数
D
分析:将函数解析式第一项利用完全平方公式展开,利用同角三角函数间的基本关系及二倍角的正弦函数公式化简,抵消后得到一个角的正弦函数,由正弦函数为奇函数得到此函数为奇函数,找出ω的值,代入周期公式T=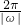 即可求出函数的最小正周期.
即可求出函数的最小正周期.
解答:y=(sinx-cosx)2-1
=sin2x-2sinxcosx+cos2x-1
=(sin2x+cos2x)-1-sin2x
=-sin2x,
∵正弦函数为奇函数,可得出y=-sin2x为奇函数,
又ω=2,
∴T= =π,
=π,
则原函数为周期是π的奇函数.
故选D
点评:此题考查了三角函数的周期性及其求法,涉及的知识有:同角三角函数间的基本关系,二倍角的正弦函数公式,正弦函数的奇偶性,以及三角函数周期公式的运用,其中利用三角函数的恒等变换将函数解析式化为一个角的正弦函数是本题求函数周期的关键.
分析:将函数解析式第一项利用完全平方公式展开,利用同角三角函数间的基本关系及二倍角的正弦函数公式化简,抵消后得到一个角的正弦函数,由正弦函数为奇函数得到此函数为奇函数,找出ω的值,代入周期公式T=
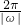 即可求出函数的最小正周期.
即可求出函数的最小正周期.解答:y=(sinx-cosx)2-1
=sin2x-2sinxcosx+cos2x-1
=(sin2x+cos2x)-1-sin2x
=-sin2x,
∵正弦函数为奇函数,可得出y=-sin2x为奇函数,
又ω=2,
∴T=
 =π,
=π,则原函数为周期是π的奇函数.
故选D
点评:此题考查了三角函数的周期性及其求法,涉及的知识有:同角三角函数间的基本关系,二倍角的正弦函数公式,正弦函数的奇偶性,以及三角函数周期公式的运用,其中利用三角函数的恒等变换将函数解析式化为一个角的正弦函数是本题求函数周期的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
已知函数y=(sinx+cosx)2+2cos2x,则它的最大值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|