题目内容
已知函数y=(sinx+cosx)2+2cos2x.
(1)求函数f(x)的单调递增区间.
(2)求f(x)的最小值以及取得最小值时x的集合.
(1)求函数f(x)的单调递增区间.
(2)求f(x)的最小值以及取得最小值时x的集合.
分析:(1)利用三角函数中的恒等变换可将y=f(x)=(sinx+cosx)2+2cos2x转化为f(x)=
sin(2x+
)+2,从而可求f(x)的单调递增区间.
(2)由(1)知f(x)=
sin(2x+
)+2,利用正弦函数的性质可求f(x)的最小值以及取得最小值时x的集合.
| 2 |
| π |
| 4 |
(2)由(1)知f(x)=
| 2 |
| π |
| 4 |
解答:解:(1)∵y=(sinx+cosx)2+2cos2x
=1+sin2x+1+cos2x
=
sin(2x+
)+2,
∴由2kπ-
≤2x+
≤2kπ+
得:kπ-
≤x≤kπ+
(k∈Z),
∴函数f(x)的单调递增区间为[kπ-
,kπ+
](k∈Z);
(2)∵f(x)=
sin(2x+
)+2,
∴当2x+
=2kπ-
,即x=kπ-
(k∈Z)时,f(x)取得最小值2-
.
即f(x)取得最小值时x的集合为{x|x=kπ-
(k∈Z)}.
=1+sin2x+1+cos2x
=
| 2 |
| π |
| 4 |
∴由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| π |
| 8 |
∴函数f(x)的单调递增区间为[kπ-
| 3π |
| 8 |
| π |
| 8 |
(2)∵f(x)=
| 2 |
| π |
| 4 |
∴当2x+
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| 2 |
即f(x)取得最小值时x的集合为{x|x=kπ-
| 3π |
| 8 |
点评:本题考查三角函数中的恒等变换应用,考查正弦函数的单调性与最值,考查运算能力,属于中档题.

练习册系列答案
相关题目
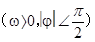 的部分图象如图所( )
的部分图象如图所( )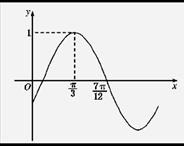
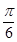 B.ω=1,φ=-
B.ω=1,φ=-