题目内容
已知函数y=（sinx+cosx）2+2cos2x，则它的最大值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析：把函数解析式的第一项利用完全平方公式展开，根据条件三角函数间的基本关系及二倍角的正弦函数公式化简，第二项利用二倍角的余弦函数公式化简，再提取
，利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数，根据x属于R，根据正弦函数的值域求出正弦函数的最大值，进而得到函数的最大值．
| 2 |
解答：解：函数y=（sinx+cosx）2+2cos2x
=sin2x+cos2x+2sinxcosx+cos2x+1
=2+sin2x+cos2x
=2+
sin（2x+
），
∵x∈R，∴-1≤sin（2x+
）≤1，
则函数的最大值为2+
．
故选D
=sin2x+cos2x+2sinxcosx+cos2x+1
=2+sin2x+cos2x
=2+
| 2 |
| π |
| 4 |
∵x∈R，∴-1≤sin（2x+
| π |
| 4 |
则函数的最大值为2+
| 2 |
故选D
点评：此题考查了二倍角的正弦、余弦函数公式，同角三角函数间的基本关系，正弦函数的值域以及两角和与差的正弦函数公式，灵活运用三角函数的恒等变形把函数解析式化为一个角的正弦函数是解本题的关键．
练习册系列答案
相关题目
)的图象上各点的横坐标伸长到原来的3倍，再向右平移
个单位，得到的函数的一个对称中心是
，0)
，0)
，0)
，0)
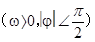的部分图象如图所( )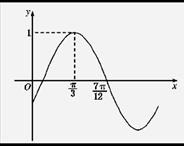
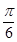B．ω＝1，φ＝－
＋
cos