Question

若a是从区间[0，10]中任取的一个实数，则方程x²-ax+1=0无实解的概率是________．

Answer 1

分析：根据题意先确定是几何概型中的长度类型，由方程x²-ax+1=0无实解，则必须有△＜0，求出构成的区域长度，再求出在区间[0，10]上任取一个数a构成的区域长度，再求两长度的比值．
解答：方程x²-ax+1=0无实解，
则：△=a²-4＜0，
即：（a-2）（a+2）＜0，?-2＜a＜2，
又a≥0，
∴0≤a＜2，其构成的区域长度为2，
从区间[0，10]中任取的一个实数a构成的区域长度为10，
则方程x²-ax+1=0无实解的概率是=
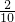故答案为：．
点评：本题主要考查概率的建模和解模能力，本题是长度类型，思路是先求得试验的全部构成的长度和构成事件的区域长度，再求比值．